মডেল অ্যাক্টিভিটি টাস্ক
নবম শ্রেণি
গণিত
নীচের প্রশ্নগুলির উত্তর লেখো:
1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs) :
(i) শতকরা লাভ 10 হলে, ক্রয়মূল্য ও বিক্রয়মূল্যের অনুপাত হবে-
(a) 1 : 10
(b) 10 : 1
(c) 10 : 11
(d) 11 : 10
উত্তর: (c) 10 : 11
(ii) ΔABC-এর AB বাহুর মধ্যবিন্দু D দিয়ে BC-এর সমান্তরাল DE টানা হলো যা AC বাহুকে E বিন্দুতে ছেদ করলো, তাহলে-
(a) AE= 1/3 AC
(b) AE= 1/2 AC
(c) AE= 1/4 AC
(d) AE= 2/3 AC
উত্তর: (b) AE= 1/2 AC
(iii) যে অর্ধবৃত্তাকার চাকতির ব্যাসার্ধের দৈর্ঘ্য 10.5 সেমি. তার পরিসীমা হলো
(a) 2π × 10.5 সেমি.
(b) (π+2) × 10.5 সেমি.
(c) 2(π+1) × 10.5 সেমি.
(d) (π+1) × 10.5 সেমি.
উত্তর: (b) (π+2) × 10.5 সেমি.
(iv) যে বর্গাকার চিত্রে কর্ণের দৈর্ঘ্য 13√2 সেমি., তার একটি বাহুর দৈর্ঘ্য হবে
(a) 13√2/2 সেমি.
(b) 26 সেমি.
(c) √338 সেমি.
(d) 13 সেমি.
উত্তর: (d) 13 সেমি.
2. সত্য/মিথ্যা লেখো (T/F):
(i) ধার্যমূল্যের উপর ছাড় নির্ভর করে।
উত্তর: সত্য
(ii) পরিসংখ্যা বহুভুজ অঙ্কনের জন্য প্রথম শ্রেণির ঠিক আগের একটি শ্রেণির পরিসংখ্যা হবে ‘0’।
উত্তর: সত্য
(iii) 
চিত্রে ABCD বর্গক্ষেত্রের ক্ষেত্রফল ABEF রসম্ব আকার ক্ষেত্রের ক্ষেত্রফলের সমান।
উত্তর: মিথ্যা
(iv) প্রতিটি বৃত্তের পরিধি ও ব্যাসের দৈর্ঘ্যের অনুপাত একটি নির্দিষ্ট সংখ্যা।
উত্তর: সত্য
ব্যাখ্যা : কোনো বৃত্তের ব্যাসার্ধ। হলে, সেই বৃত্তটির
পরিধি = 2πr এবং ব্যাস=2r
∴ বৃত্তের পরিধি : বৃত্তের ব্যাস
= 2πr : 2r
= π : 1
অর্থাৎ, বৃত্তের পরিধি ও ব্যাসের দৈর্ঘ্যের অনুপাত সর্বদা π হবে যা একটি নির্দিষ্ট সংখ্যা |
3.সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন:
(i) 10 টি পেনের ক্রয়মূল্য ৪টি পেনের বিক্রয়মূল্যের সমান হলে, শতকরা লাভ কত ?
উত্তর: ধরি, 10 টি পেনের ক্রয়মূল্য = 100 টাকা
∴ ৪ টি পেনের বিক্রয়মূল্য = 100 টাকা
1 টি পেনের বিক্রয়মূল্য = 100/8 টাকা
10 টি পেনের বিক্রয়মূল্য = (100/8) × 10 টাকা
= 125 টাকা
∴ 10 টি পেন বিক্রয় করে মোট লাভ = (125 – 100)
= 25 টাকা
∴ শতকরা লাভ = (25/100) × 100 %
= 25 ( উত্তর )
(ii)
| শ্রেণি সীমা | 70-74 | 75-79 | 80-84 | 85-89 |
| পরিসংখ্যা | 3 | 4 | 5 | 8 |
উপরের পরিসংখ্যা বিভাজন তালিকার প্রথম শ্রেণির পরিসংখ্যা ঘনত্ব নির্ণয় করো ।
উত্তর: প্রথম শ্রেণির শ্রেণি সীমা = 70-74
∴ প্রথম শ্রেণির শ্রেণি সীমানা = 69.5-74.5
∴ প্রথম শ্রেণির শ্রেণি দৈর্ঘ্য (D) = 74.5 – 69.5 = 5
প্রথম শ্রেণির পরিসংখ্যা (F) = 3
∴ প্রথম শ্রেণির পরিসংখ্যা ঘনত্ব (D) =F/D
= 3/5 = 0.6 (উত্তর)
(iii) 
চিত্রে, ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 96 বর্গমি. এবং ভূমি BC = 20 মি. হলে, ত্রিভুজটির উচ্চতা h মি. নির্ণয় করো।
উত্তর: আমরা জানি,
ত্রিভুজের ক্ষেত্রফল = (1/2) × ভূমি × উচ্চতা
বা, 96 = (1/2) × 20 × h
বা, 96 × 2 × (1/20) = h
বা, 96/10 = h
বা, h = 9.6
∴ ত্রিভুজটির উচ্চতা 9.6 মিটার (উত্তর)
4. সমদ্বিবাহু ত্রিভুজ অঙ্কন করো যার সমান বাহু দুটির প্রত্যেকটির দৈর্ঘ্য ৪ সেমি এবং সমান বাহু দুটির অন্তর্ভুক্ত 30° কোণ ওই ত্রিভুজটির সমান ক্ষেত্রফল বিশিষ্ট একটি আয়তক্ষেত্র অঙ্কন করো।
উত্তর:
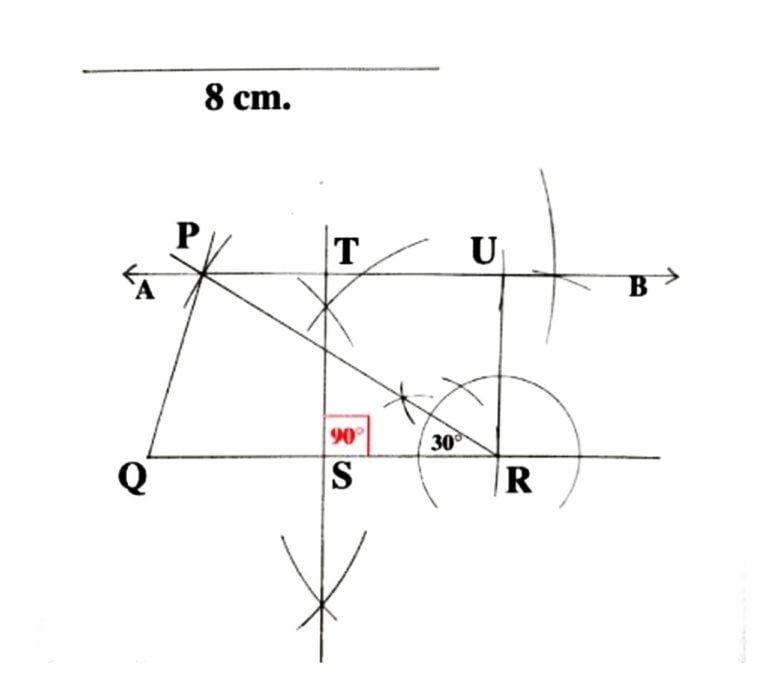
PQR একটি সমদ্বিবাহু ত্রিভুজ অঙ্কন করলাম যার সমান বাহু দুটি হলো PR = QR = 8 সেমি. এবং সমান বাহু দুটির অন্তর্ভুক্ত কোণ ∠SRU = 30° | এই PQR সমদ্বিবাহু ত্রিভুজের সমান ক্ষেত্রফলবিশিষ্ট একটি আয়তক্ষেত্র RSTU অঙ্কনকরা হলো |
অথবা,
নীচের পরিসংখ্যা বিভাজন ছকটির পরিসংখ্যা বহুভুজ অঙ্কন করো ।
| শ্রেণি | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
| পরিসংখ্যা | 4 | 10 | 24 | 12 | 20 | 8 |
উত্তর:
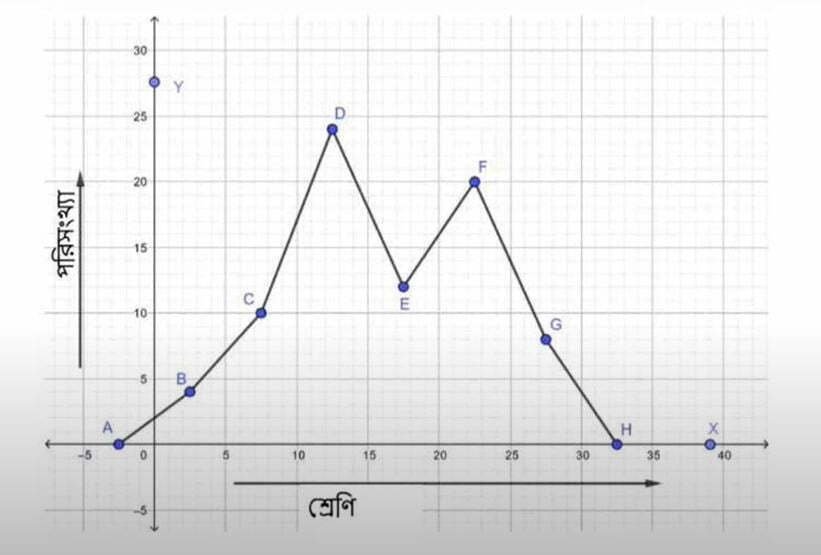
x-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহু = 1 একক এবং y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহু = 1 একক ধরলাম।
এরপর ছক কাগজে (-2.5,0), (2.5,4), (7.5,10), (12.5,24), (17.5,12), (22.5,20), (27.5,4), (32.5,0) বিন্দুগুলি পরপর সরলরেখাংশ দ্বারা যােগ করে ABCDEFGH পরিসংখ্যা বহুভুজটি অঙ্কন করলাম।
Class 9 Model Activity Task Part 7 October
Bangla (বাংলা) | Math (গণিত) | ENGLISH (ইংরেজি) | Geography (পরিবেশ ও ভূগোল) | History (ইতিহাস) | Life Science (জীবনবিজ্ঞান) | Physical Science (ভৌতবিজ্ঞান)
Class 9 Model Activity Task Part 6 September
Bangla (বাংলা) | Math (গণিত) | ENGLISH (ইংরেজি) | Geography (পরিবেশ ও ভূগোল) | History (ইতিহাস) | Life Science (জীবনবিজ্ঞান) | Physical Science (ভৌতবিজ্ঞান)
Note: এই আর্টিকেলের ব্যাপারে তোমার মতামত জানাতে নীচে দেওয়া কমেন্ট বক্সে গিয়ে কমেন্ট করতে পারো। ধন্যবাদ।