Class 10 Mathematics Model Activity Task Part 8 Combined Answer 2021 | দশম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট ৮

প্রিয় ছাত্রছাত্রীরা, এই আর্টিকেলে আমরা নবম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট ৮ (Class 10 Mathematics Model Activity Task Part 8 Combined) এর সমস্ত প্রশ্ন ও উত্তর নিয়ে এসেছি । ২০২১ এর জুলাই থেকে অক্টোবর মাস পর্যন্ত যে সমস্ত মডেল অ্যাক্টিভিটি টাস্ক দেওয়া হয়েছিল সেখান থেকে বাছাই করা করা কিছু প্রশ্ন নিয়ে এবার তোমাদের কম্বাইন্ড অ্যাক্টিভিটি টাস্ক করতে দেওয়া হয়েছে ।

Class 10 Mathematics Model Activity Task Part 8 Combined

২০২১ এর এটাই সর্বশেষ অ্যাক্টিভিটি টাস্ক । এই অ্যাক্টিভিটি টাস্কে ৫০ নম্বরের প্রশ্ন দেওয়া রয়েছে যেগুলো তোমাদের সমাধান করে বিদ্যালয়ে জমা দিতে বলা হয়েছে । এর উপর ভিত্তি করেই সম্ভাবত তোমরা পরবর্তী শ্রেণীতে উত্তীর্ণ হবে । সুতরাং, খুবই মন দিয়ে তোমরা নিচের প্রশ্নোত্তর গুলি পড়বে এবং লিখবে ।

মডেল অ্যাক্টিভিটি টাস্ক Part 8 (Combined), October 2021

গণিত (পূর্ণমান ৫০)

দশম শ্রেণী

Class 10 Mathematics Model Activity Task Part 8 Solution :

নীচের প্রশ্নগুলির উত্তর লেখাে : 

1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs)

(i) বাস্তব সহগ যুক্ত একচলবিশিষ্ট দ্বিঘাত সমীকরণটি হলাে 

(a) x(x² – 1) – 3x = 0

(b) x²(x² – 1) – 6x = 0 

(c) x(x-1) – x = 0

(d) 2x – 4 = 0 

উত্তর: (c) x(x-1) – x = 0

(ii) (2x -2) (x + 3) = 0 সমীকরণটির বীজ দুটি হলাে 

(a) -1, -3

(b) -1, 3 

(c) 1,-3

(d) 1, 3 

উত্তর: (c) 1,-3

(iii) বার্ষিক 10% সরল সুদের হারে 50 টাকার 2 বছরের সুদ ঐ একই হারে 100 টাকার 1 বছরের সুদের 

(a) দ্বিগুণ

(b) অর্ধেক 

(c) এক চতুর্থাংশ

(d) সমান

উত্তর: (d) সমান

(iv) O কেন্দ্রীয় বৃত্তের PQও RS দুটি সমান দৈর্ঘ্যের জ্যা। O বিন্দু থেকে PQ জ্যা-এর দূরত্ব 8 সেমি হলে, O বিন্দু থেকে RS জ্যা-এর দূরত্ব হবে 

(a) 8 সেমি.

(b) 16 সেমি. 

(c) 4 সেমি.

(d) 10 সেমি. 

উত্তর: (a) 8 সেমি.

(v) O কেন্দ্রীয় বৃত্তের বহিঃস্থ P বিন্দু থেকে অঙ্কিত স্পর্শক বৃত্তকে Q বিন্দুতে স্পর্শ করে। OQ = 9 সেমি, PO = 15 সেমি. হলে PQ-এর দৈর্ঘ্য হবে

(a) 6 সেমি 

(b) `\sqrt{15^2-9^2}` সেমি 

(c) `\sqrt{15^2+9^2}` সেমি

(d) 13 সেমি 

উত্তর: (b) `\sqrt{15^2-9^2}` সেমি

(vi) দুটি নিরেট গােলকের বক্রতলের ক্ষেত্রফলের অনুপাত 25 : 16 হলে, তাদের আয়তনের অনুপাত হবে 

(a) 5:4 

(b) 64 : 125 

(c) 4:5

(d) 125 : 64 

উত্তর: (d) 125 : 64 

(vii) দুটি বৃত্ত পরস্পরকে C বিন্দুতে বহিঃস্পর্শ করে। AB বৃত্ত দুটির একটি সাধারণ স্পর্শক বৃত্তদুটিকে A ও B বিন্দুতে স্পর্শ করে, ∠ACB-এর পরিমাপ হলাে, 

(a) 60°

(b) 45°

(c) 30°

(d) 90°

উত্তর: (d) 90°

(viii) একটি নিরেট অর্ধগােলকের সমগ্রতলের ক্ষেত্রফল 147Π বর্গসেমি. হলে, উহার ব্যাসার্ধ হবে, 

(a) 6 সেমি.

(b) 12 সেমি. 

(c) 7 সেমি.

(d) 14 সেমি.

উত্তর: (c) 7 সেমি.

2. সত্য/মিথ্যা (T/F) লেখাে :

(i) একটি ঘনকের প্রতিটি ধারের দৈর্ঘ্য অর্ধেক করা হলে, ঘনকটির আয়তন প্রথম ঘনকের আয়তনের `\frac1{8}` অংশ হবে।

উত্তর: সত্য

(ii) `\frac{a}{2}=\frac{b}{3}=\frac{c}{4}` হলে, a:b:c = 4:3:2 হবে।

উত্তর: মিথ্যা

(iii) আসল P টাকা এবং বার্ষিক চক্রবৃদ্ধি সুদের হার r% হলে, দ্বিতীয় বছরের মূলধন `\frac{Pr}{100}` টাকা।

উত্তর: মিথ্যা

(iv) 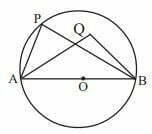চিত্রে O কেন্দ্রবিশিষ্ট বৃত্তে AB একটি ব্যাস। বৃত্তের ভেতরে Q একটি বিন্দু। ∠AQB সর্বদা সূক্ষ্মকোণ হবে।

উত্তর: মিথ্যা

(v) Δ ABC-এর BC বাহুর উপর D এমন একটি বিন্দু যে AD ⊥ BC; সুতরাং Δ ABD ∼ Δ CAD

উত্তর: মিথ্যা

(vi) শুভেন্দু ও নৌসদ যথাক্রমে 1500 টাকা এবং 1000 টাকা দিয়ে একটি ব্যবসা শুরু করে। এক বছর পরে ব্যবসায় 75 টাকা ক্ষতি হলে, শুভেন্দুর ক্ষতি হয় 30 টাকা।

উত্তর: মিথ্যা

(vii) পাশের চিত্রে ST | | QR হলে, `\frac{PQ}{PS}` = `\frac{PR}{PT}` হবে।

উত্তর: সত্য

(viii) শঙ্কুর তির্যক উচ্চতা শঙ্কুর উচ্চতার দ্বিগুণ হলে, শঙ্কুর ব্যাসার্ধ হবে, উচ্চতা × `\sqrt{3}`

উত্তর: সত্য

3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A) :

(i) একটি লম্ব বৃত্তাকার চোঙের আয়তন এবং তলের ক্ষেত্রফল সাংখ্যমানে সমান হলে, উহার ব্যাসার্ধ নির্ণয় করাে। 

উত্তর: ধরি, লম্ব বৃত্তাকার চোঙের ভূমির ব্যাসার্ধ = r একক এবং উচ্চতা = h একক

∴ লম্ব বৃত্তাকার চোঙের আয়তন = πr²h ঘনএকক

∴ লম্ব বৃত্তাকার চোঙের বক্রতলের ক্ষেত্রফল = 2πrh বর্গএকক

∴ প্রশ্নানুসারে, πr²h = 2πrh

বা, r₂ = 2r

বা, r = 2

∴ লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ = 2 একক

(ii) দেখাও যে, মিশ্র দ্বিঘাত করণী `(7-\sqrt2)`-এর অনুবন্ধী করণী হলাে `(7+\sqrt2)`  

উত্তর: `(7-\sqrt2)` ও `(7+\sqrt2)` -এর যোগফল ও গুণফল উভয়ই যদি মূলদ সংখ্যা হয় তাহলে `(7+\sqrt2)` কে বলা হবে `(7-\sqrt2)` এর অনুবন্ধী করনী

∴ `(7-\sqrt2)` + `(7+\sqrt2)` = 14, এটি মূলদ সংখ্যা

∴ `(7-\sqrt2)` × `(7+\sqrt2)` = `(7)^2-(\sqrt2)^2` = 49 – 2 = 47, এটি মূলদ সংখ্যা

∴ আমরা বলতে পারি, `(7-\sqrt2)` এর অনুবন্ধী করনী `(7+\sqrt2)`

(iii) একটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতা 12 সেমি. এবং আয়তন 100 ∏ ঘন সেমি হলে, শঙ্কুটির ব্যাসার্ধের দৈর্ঘ্য কত তা নির্ণয় করাে। 

উত্তর: লম্ব বৃত্তাকার শঙ্কুর উচ্চতা (h) = 12 সেমি.

লম্ব বৃত্তাকার শঙ্কুর আয়তন = 100π ঘন সেমি.

ধরি শঙ্কুর ব্যাসার্ধ = r সেমি.

∴ প্রশ্নানুসারে, `\frac1{3}πr^2h=100\pi`

বা, `r^2h=100\times3`

`r=\sqrt{\frac{100\times\cancel3}{\underset4{\cancel{12}}}}=\sqrt{\frac{100}4}=\frac10{2}`

বা, r = 5

∴ শঙ্কুর ভুমির ব্যাসার্ধ 5 সেমি.

(iv) x ∝ yz এবং y ∝ zx হলে, দেখাও যে, z একটি অশূন্য ধ্রুবক। 

উত্তর: x ∝ yz

∴ x = k₁yz —(i)

k₁ = অশূন্য ভেদ ধ্রুবক

y ∝ zx

∴ y = k₂zx —(i)

k₂ = অশূন্য ভেদ ধ্রুবক

(i) ও (ii) গুন করে পাই

∴ `x.y=k_1.yz.k_2.zx`

`xy=k_1.k_2.xyz^2`

`z^2=\frac1{k_1k_2}`

`z=\pm\sqrt{\frac1{k_1k_2}}=` ভেদ ধ্রুবক

(v) তিন বন্ধু A, B এবং C একসঙ্গে কিছু মূলধন নিয়ে একটি বাস ক্রয় করেন। তারা ঠিক করেন যে মােট আয়ের `\frac2{5}` অংশ কাজের জন্য 3 : 2 : 2 অনুপাতে ভাগ করে নেবেন। কোনাে একমাসে যদি 29260 টাকা আয় হয় তাহলে কাজের জন্য A-এর আয় B-এর আয় থেকে কত বেশি হবে? 

উত্তর: একমাসে তাদের আয়ের পরিমাণ = 29260 টাকা

মোট আয়ের `\frac2{5}` অংশ `=\overset{5852}{\cancel{29260}}\times\frac2{\cancel5}` = 11704 টাকা

এই টাকা কাজের জন্য 3:2:2 অনুপাতে ভাগ করবেন

∴ A এর আয় = `11704\times\frac3{3+2+2}` = `\overset{1672}{\cancel{11704}}\times\frac3{\cancel7}` = 5016 টাকা

∴ B এর আয় = `\overset{1672}{\cancel{11704}}\times\frac2{\cancel7}` = 3344 টাকা

∴ A এর আয় B এর আয়ের থেকে = (5016-3344) = 1672 টাকা বেশি।

(vi) একটি লম্ব বৃত্তাকার চোঙ এবং লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 3:4 এবং তাদের আয়তনের অনুপাত 9:8; চোঙ ও শঙ্কুর উচ্চতার অনুপাত নির্ণয় করাে। 

উত্তর: মনে করি, লম্ব বৃত্তাকার চোঙ এবং লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ যথাক্রমে r₁ একক ও r₂ একক এবং তাদের উচ্চতা যথাক্রমে h₁ একক ও h₂ একক

∴ তাদের আয়তন যথাক্রমে πr₁²h₁ ঘন একক এবং `\frac1{3}`πr₂²h₂ ঘন একক

প্রশ্নানুসারে, r₁ : r₂ = 3 : 4

বা, `\frac{r_1}{r_2}` = `\frac3{2}`

এবং πr₁²h₁ : `\frac1{3}`πr₂²h₂ = 9 : 8

বা, `3(\frac{r_1}{r_2})^2(\frac{h_1}{h_2})=\frac9{8}`

বা, `3(\frac3{4})^2(\frac{h_1}{h_2})=\frac9{8}`

বা, `\frac{h_1}{h_2}=\frac{9\times16}{8\times9\times3}=\frac2{3}`

∴ নির্ণেয় উচ্চতার অনুপাত = 2 : 3

(vii) যদি y ∝ x³ এবং y-এর বৃদ্ধি 8:27 অনুপাতে হলে x-এর বৃদ্ধি কী অনুপাতে হয় তা নির্ণয় করাে। 

উত্তর: প্রদত্ত y ∝ x³

∴ y = kx³ [ k = অশুন্য ভেদ ধ্রুবক ]

∴ y এর বৃদ্ধি 8:27 অনুপাত হয় অর্থাৎ 

প্রথমে y = 8k₁ এবং পরে y = 27k₁ [ k₁ ≠ 0 ]

যখন y = 8k₁ তখন 8k₁ = kx³ বা, x = `2.(\frac{k_1}k)^{\frac1{3}}`

আবার y = 27k₁ তখন 27k₁ = kx³ বা, x = `3.(\frac{k_1}k)^{\frac1{3}}`

∴ x -এর বৃদ্ধির অনুপাত = `\frac{2.(\frac{k_1}k)^\frac1{3}}{3.(\frac{k_1}k)^\frac1{3}}` = `\frac2{3}` = 2:3

Read Also:

Class 10 English 2nd Language Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 10 Bengali (বাংলা প্রথম ভাষা) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 10 History (ইতিহাস) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 10 Geography (ভূগোল) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 10 Life Science (জীবন বিজ্ঞান) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 10 Physical Science (ভৌতবিজ্ঞান) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 1-10 Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

4. (i) যুক্তি দিয়ে প্রমাণ করাে যে, বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক।

উত্তর:

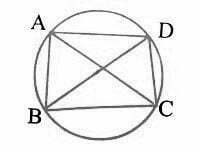
প্রদত্তঃ ABCD একটি বৃত্তস্থ চতুর্ভুজ।

প্রামাণ্য বিষয়ঃ ∠ABC+∠ADC = 2 সমকোণ।

এবং ∠BAD+∠BCD = 2 সমকোণ।

অঙ্কনঃ AC ও BD কর্ণ টানলাম।

প্রমাণঃ

∠ADB=∠ACB [একই বৃত্তের ব্যাসার্ধ]

আবার, ∠BAC=∠BDC [একই বৃত্তের ব্যাসার্ধ]

আবার, ∠ADC=∠ACB+∠BAC

∴∠ADC+∠ABC=∠ACB+∠BAC+∠ABC

∴∠ADC+∠ABC =2 সমকোণ [ ত্রিভুজের তিনটি কোণের সমষ্টি 2 সমকোণ ]

∠BAD+BCD = 2 সমকোণ [ প্রমাণিত ]

(ii) যুক্তি দিয়ে প্রমাণ করাে যে, বৃত্তের বহিঃস্থ কোনাে বিন্দু থেকে যে দুটি স্পর্শক অঙ্কন করা যায় তাদের স্পর্শবিন্দু দুটির সঙ্গে বহিঃস্থ বিন্দুর সংযােজক সরলরেখাংশ দুটির দৈর্ঘ্য সমান এবং তারা কেন্দ্রে সমান কোণ উৎপন্ন করে। 

উত্তর:

প্রদত্ত: O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু P থেকে PA ও PB দুটি স্পর্শক যাদের স্পর্শ বিন্দু যথাক্রমে A ও B, O, A;  O, B; O, P যুক্ত করায় PA ও PB সরলরেখাংশ দুটি কেন্দ্রে যথাক্রমে ㄥPOA ও ㄥPOB দুটি কোণ উৎপন্ন করেছে।

প্রমাণ করতে হবে:  (i) PA = PB, (ii) ㄥPOA = ㄥPOB

প্রমান: PA ও PB স্পর্শক এবং OA ও OB স্পর্শবিন্দুগামী ব্যাসার্ধ।

         ∴ OA 丄 PA  এবং OB 丄 PB

POA ও POB সমকোণী ত্রিভুজদ্বয়ের মধ্যে ㄥOAP = ㄥOBP (প্রত্যেকে 1 সমকোণ)

অতিভুজ OP সাধারণ বাহু এবং OA = OB (একই বৃত্তের ব্যাসার্ধ)

∴ ΔPAO ≅ ΔPBO [সর্বসমতার R-H-S শর্তানুসারে]

∴PA = PB (সর্বসম ত্রিভুজের অনুরূপ বাহু)

এবং ㄥPOA = ㄥPOB (সর্বসম ত্রিভুজের অনুরূপ কোণ)

[প্রমাণিত ]

5. (i) বার্ষিক 4% সরলসুদে কত বছরে 600 টাকার সুদ 168 টাকা হবে তা নির্ণয় করাে।

উত্তর: আসল (p) = 600 টাকা

বার্ষিক সুদের হার (r) = 4%

সুদ (I) = 168 টাকা ; ধরি, সময় = t বছর

∴ I = `\frac{prt}{100}`

বা, t = `\frac{I\times100}{pr}` =  `\frac{\overset{\overset7{\cancel{42}}}{\cancel168}\times1\cancel{00}}{\cancel6\cancel{00}\times\cancel4}` = 7 বছর

∴ বার্ষিক 4% সরল সুদে 7 বছরে 600 টাকার সুদ হবে 168 টাকা।

(ii) কত টাকা বার্ষিক 5% চক্রবৃদ্ধিহার সুদে 2 বছর পরে সুদে আসলে 3528 টাকা হবে।

উত্তর: ধরি, আসল (p) = x টাকা

সুদের হার (r) = 4% ; সময় (n) = 2 বছর

এবং সুদ আসল (A) = 3528 টাকা

আমরা জানি, A = `p(1+\frac r{100})^n`

বা, 3528 = `p(1+\frac5{100})^2` = `p(\frac{105}{100})^2`

বা, p = `\frac{\overset{\overset8{\cancel168}}{\cancel{3528}}\times100\times\overset{\overset4{\cancel20}}{\cancel100}}{\underset{\cancel21}{\cancel105}\times\underset{\cancel21}{\cancel105}}`

বা, p = 3200 টাকা

∴ 3200 টাকার সুদে আসলে 3528 টাকা হবে