এই আর্টিকেলে আমরা মাধ্যমিক গণিত সমাধান Theorems related to Angles Koshe Dekhi 7.2 নিয়ে এসেছি। Class 10 Theorems related to Angles Koshe Dekhi 7.2 Answer solve | Class X Theorems related to Angles Koshe Dekhi 7.2 | মাধ্যমিক গণিতের সপ্তম অধ্যায় বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.২ থেকে সমস্ত প্রশ্ন ও উত্তর নিয়ে এখানে আলোচনা করা হয়েছে। মাধ্যমিক গণিত প্রকাশ বইয়ের সমস্ত অধ্যায়ের উত্তর পেতে এই লিঙ্কে ক্লিক করো।
বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য
Theorems related to Angles in a Circle
কষে দেখি ৭.২
Class 10 Theorems related to Angles Koshe Dekhi 7.2 Solution
1. পাশের ছবিতে ∠DBA =40° ,∠BAC= 60° এবং ∠CAD=20°; ∠DCA ও ∠BCA এর মাণ নির্ণয় করি । ∠BAD ও ∠DCB এর মানের সমষ্টি কত হবে তা হিসাব করে দেখি ।
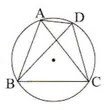
সমাধানঃ ∠DBA =40° ,∠BAC= 60° এবং ∠CAD=20°
∠DBA=∠DCA=40° [∵ একই বৃত্যাংশস্থ সকল কোণের মাণ সমান ]
ত্রিভুজ ABD এর ক্ষেত্রে ,
∠ABD+∠ADB+∠BAD=180° [∵ ত্রিভুজের তিনটি কোণের সমষ্টি 180°]
বা, ∠ABD+∠BAC+∠CAD+∠ADB=180°
বা, 40+60+20+∠ADB=180°
বা, ∠ADB=180°-120°
বা, ∠ADB = 60°
আবার, ∠ADB=∠BCA= 60° [∵ একই বৃত্যাংশস্থ সকল কোণের মাণ সমান ]
∴ ∠DCA=40° এবং ∠BCA= 60°[উত্তর ]
এখন, ∠BAD+∠DCB
= ∠BAC+∠CAD+∠DCA+∠ACB
= 60°+20°+40°+60°
=180°
∴ ∠BAD+∠DCB= 180° (উত্তর)
2.পাশের চিত্রে AOB বৃত্তের ব্যাস এবং বৃত্তের কেন্দ্র O । OC ব্যাসার্ধ AB এর ওপর লম্ব । যদি উপচাপ CB এর উপর কোনো বিন্দু P হয় , তবে ∠BAC ও ∠APC এর মাণ হিসাব করে লিখি ।
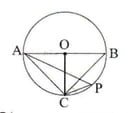
সমাধানঃ
OC ⊥ AB
∴ AOC = 90°
এখন , △AOC এর ক্ষেত্রে ,
OA=OC [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠OAC =∠OCA
আবার, ∠OAC+∠OCA=90° [∵ ∠AOC=90°]
∴∠OAC+∠OAC= 90° [∵∠OAC =∠OCA]
বা, 2∠OAC=90°
বা, ∠OAC = 45°
∴ ∠BAC=45°
একই ভাবে ত্রিভুজ △OBC থেকে পাই ,
OB=OC [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠OBC=∠OCB
আবার , ∠OBC+∠OCB=90°[ ∵BOC = 90° কারণ OC⊥AB]
∴ ∠OBC+∠OBC=90°[∵ ∠OBC=∠OCB]
বা, ∠OBC= 45°
বা, ∠ABC=45°
আবার, ∠ABC = ∠APC=45° [ ∵ একই বৃত্যাংশস্থ কোণের মাণ সমান]
∴ ∠APC=45°
∴ ∠BAC=45° এবং ∠APC=45° (উত্তর)
3.ABC ত্রিভুজের O লম্ববিন্দু এবং BC –এর উপর অঙ্কিত লম্ব AD-কে বর্ধিত করলে △ABC এর পরিবৃত্ত কে G বিন্দুতে ছেদ করে । প্রমাণ করি OD =DG ।

△ABC ত্রিভুজের O লম্ববিন্দু । অর্থাৎ , লম্বত্রয় AD , BE এবং CF পরস্পরকে O বিন্দুতে ছেদ করেছে । BC এর উপর অঙ্কিত লম্ব AD কে বর্ধিত করলে ABC পরিবৃত্ত কে G বিন্দুতে ছেদ করে , প্রমাণ করতে হবে , OD = DG
অঙ্কনঃ C,G ; B,G যুক্ত করা হল ।
প্রমাণঃ ∠ACB এবং ∠AGB একই বৃত্যাংশস্থ কোণ
∴ ∠ACB = ∠AGB
∴ ∠ECB = ∠OGB —-(i)
OECD চতুর্ভুজের ক্ষেত্রে ,
এখন , ∠OEC=∠ODC = 90°[∵OE এবং OD যথাক্রমে AC এবং BC বাহুর ওপর লম্ব ]
∴ ∠DOE +∠DCE = 180° [ ∵চতুর্ভুজের চারটি কোণের সমষ্টি 360°]
∴ ∠GOE+∠ECB=180°—-(ii)
আবার , OG,BE বাহুর ওপর দণ্ডায়মান
∴ ∠BOG+∠GOE = 180°—-(iii)
(ii) ও (ii) থেকে পাই ,
∠GOE+∠ECB= ∠BOG+∠GOE
∠ECB= ∠BOG—(iv)
আবার, (i) ও (iv) থেকে পাই ,
∠BOG=∠OGB
∴ ∠BOD=∠BGD
এখন , ত্রিভুজ ∆BOD ও ত্রিভুজ ∆BGD থেকে পাই ,
∠BOD=∠BGD
∠BDO = ∠BDG [ উভয়ই 90°]
BD সাধারণ বাহু
∴ ∆BOD ≅ ∆BGD
∴ OD= DG [প্রমাণিত]
4. ABC –এর অন্তবৃত্তের কেন্দ্র I ; বর্ধিত AI ত্রিভুজের পরিবৃত্ত কে P বিন্দুতে ছেদ করে । প্রমাণ করি যে , PB=PC=PI
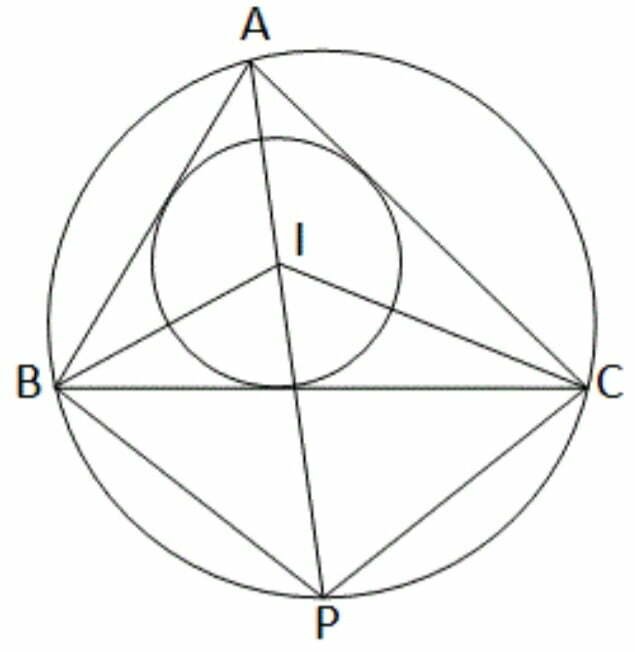
∆ABC –এর অন্তবৃত্তের কেন্দ্র I । AI কে বর্ধিত করলে তা পরিবৃত্ত কে P বিন্দুতে ছেদ করে ।
প্রমাণ করতে হবে , PB=PC=PI
অঙ্কনঃ AI,BI,CI,PB এবং PC অঙ্কন করা হল ।
প্রমাণঃ I, ABC ত্রিভুজের অন্তঃকেন্দ্র ।
∴ AI,BI ও CI ত্রিভুজের তিনটি কোণের সমদ্বিখণ্ডক ।
∠PBC = ∠PAC [ একই বৃত্যাংশস্থ কোণ ]
আবার, ∠PAC= `\frac{1}{2}` ∠BAC [ যেহেতু , AI , BAC এর সমদ্বিখণ্ডক ]
∴ ∠PBC = `\frac{1}{2}`∠BAC [∵∠PBC = ∠PAC]
এখন, ∠IBP = ∠IBC+∠PBC
বা, ∠IBP = `\frac{1}{2}`∠ABC+ `\frac{1}{2}`∠BAC——(i)
আবার , ∠ABI এর বহিঃস্থ কোণ ∠BIP
এবং ত্রিভুজের কোনো বহিঃস্থ কোণ , অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ।
∴ ∠BIP
= ∠IBA+∠IAB
= `\frac{1}{2}`∠ABC+ `\frac{1}{2}`∠BAC—-(ii)
(i) ও (ii) থেকে পাই ,
∠IBP=∠BIP
∴ ∆BIP এর PI=PB—-(iii)
অনুরূপে , ∆CIP থেকে পাই ,
PC=PI—–(iv)
(iii) ও (iv) থেকে পাই ,
PB=PC=PI [প্রমাণিত]
5.তিমির দুটি বৃত্ত এঁকেছে যারা পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে । P বিন্দু দিয়ে দুটি সরলরেখা টানলাম যারা একটি বৃত্ত কে A , B বিন্দুতে এবং অপর বৃত্তকে C ও D বিন্দুতে ছেদ করল । প্রমাণ করি যে ∠AQC = ∠BQD
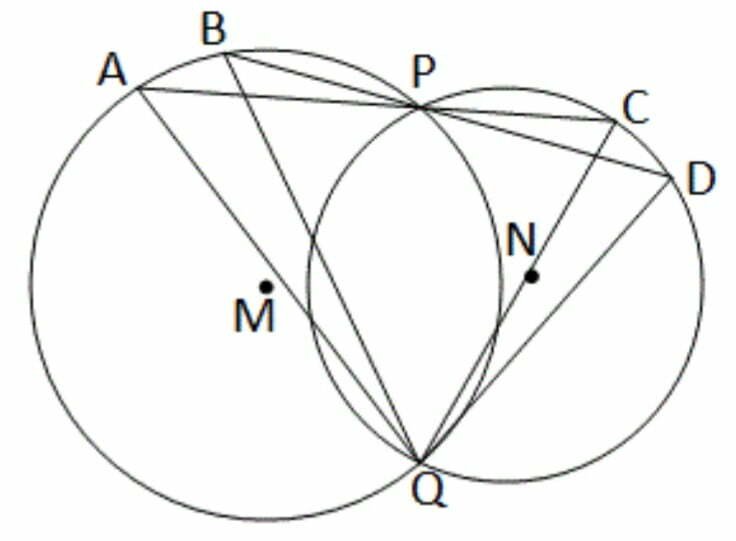
ধরি, X ও Y কেন্দ্রীয় বৃত্ত দুটি পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে । P বিন্দু দিয়ে অঙ্কিত দুটি সরলরেখা M কেন্দ্রীয় বৃত্তকে A ও B বিন্দুতে এবং N কেন্দ্রীয় বৃত্তকে C ও D বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে, ∠AQC = ∠BQD
প্রমাণঃ M কেন্দ্রীয় বৃত্তের ক্ষেত্রে ,
∠PAQ = ∠PBQ [ ∵একই বৃত্যাংশস্থ সকল কোণের মাণ সমান ]
আবার, N কেন্দ্রীয় বৃত্তের ক্ষেত্রে ,
∠PCQ = ∠PDQ [ ∵একই বৃত্যাংশস্থ সকল কোণের মাণ সমান ]
∴ ∠PAQ+∠PCQ=∠PBQ+∠PDQ —–(i)
∆AQC এর ক্ষেত্রে ,
∠AQC = 180° – (∠PAQ+∠PCQ)
= 180° -(∠PBQ+∠PDQ) [ (i) থেকে পাই ]
= ∠BQD
∴ ∠AQC = ∠BQD [প্রমাণিত]
6. একটি বৃত্তের AB ও CD জ্যা দুটি পরস্পর লম্ব । AB ও CD জ্যা দুটির ছেদবিন্দু P থেকে AD ওপর অঙ্কিত লম্বকে বর্ধিত করলে সেটি BC কে E বিন্দুতে ছেদ করে , তবে প্রমাণ করি যে E ,BC এর মধ্যবিন্দু ।
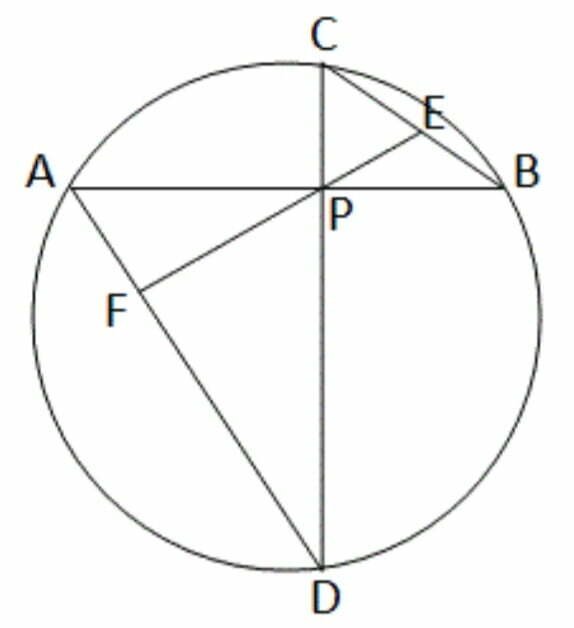
AB এবং CD জ্যা দুটি পরস্পরকে P বিন্দুতে ছেদ করেছে । P বিন্দু দিয়ে AD এর ওপর লম্ব PF; FP কে বর্ধিত করলে তা BC কে E বিন্দুতে ছেদ করে । প্রমাণ করতে হবে যে , E , BC এর মধ্যবিন্দু ।
প্রমাণঃ ∆FPD এর PF ⊥ FD
সুতরাং , ∠FPD = 90° –∠FDP
আবার , ∆APD এর AP ⊥ PD
সুতরাং, ∠PAD = 90° –∠ADP
বা, ∠PAD = 90° –∠FDP
∴ ∠FPD = ∠PAD —-(i)
অনুরূপে পাই ,
∠APF = ∠FDP—-(ii)
AC বৃত্তাংশের ওপর অবস্থিত দুটি কোণ ∠ADC এবং ∠ABC
∴ ∠ADC = ∠ABC
এবং DB বৃত্তাংশের ওপর অবস্থিত দুটি কোণ ∠DAB এবং ∠BCD
∴ ∠DAB = ∠BCD
∆CPE এর ,
∠PCE=∠PAD [ একই বৃত্যাংশস্থ কোণ ]
∠CPE = বিপ্রতীপ কোণ ∠FPD =∠PAD [ (i) নং সমীকরণ থেকে পাই ]
∴ ∠PCE = ∠CPE
সুতরাং, CE = PE —-(iii)
∆PBE এর ,
∠EBP=∠ADC [ একই বৃত্তাংশস্থ কোণ]—(iv)
∠BPE= বিপ্রতীপ∠APF=∠FDP[(ii)নংসমীকরণ থেকে পাই]—-(v)
আবার, ∠FDP=∠ADC [একই কোন]—-(vi)
(v) ও (vi) থেকে পাই,
∴∠BPE=∠ADC—(vii)
(iv) ও (vii) থেকে পাই,
∴∠EBP=∠BPE
সুতরাং, BE=PE —-(iv)
(iii) ও (iv) নং সমীকরণ থেকে পাই ,
CE=BE
∴ E , BC এর মধ্যবিন্দু [প্রমাণিত] ।
7. যদি ABCD বৃত্তস্থ চতুর্ভুজের AB =DC হয় , তবে প্রমাণ করি যে , AC = BD হবে ।
Ans. মনে করি, ABCD একটি বৃত্তস্থ চতুর্ভুজ যার AB=DC.ACও BD অঙ্কন করা হল। AC ও BD পরস্পর O বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে যে, AC=BD.
প্রমাণ :


এখানে ∠ABD=∠ACDএবং ∠BAC =∠BDC) (একই বৃত্তাংশস্থ কোণ)
এখন ΔAOB এবং ΔCOD-এর মধ্যে, ∠ABO=∠OCD, ∠BAO=∠ODC এবং AB=DC.
∴ΔAOB=ΔCOD
∴AO=OD এবং OB=0C
∴(AO+OC)=(OB+OD)
∴AC=BD
8. O কেন্দ্রীয় বৃত্তে OA ব্যাসার্ধ এবং AQ একটি জ্যা । বৃত্তের ওপর C একটি বিন্দু । O ,A,C বিন্দুগামী বৃত্ত AQ জ্যা কে P বিন্দুতে ছেদ করে ।প্রমাণ করি যে , CP =PQ
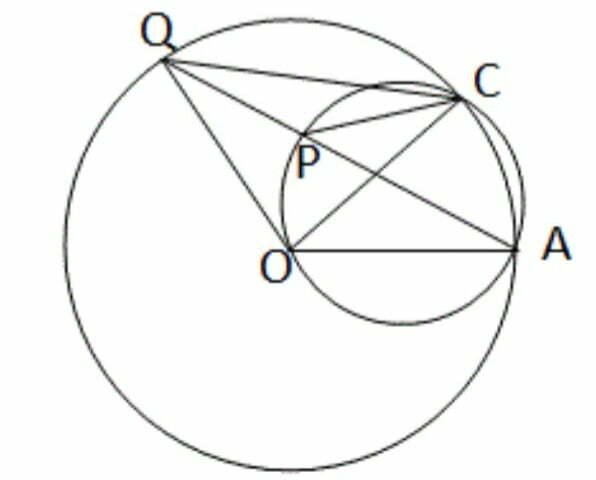
O কেন্দ্রীয় বৃত্তে OA ব্যাসার্ধ OQ একটি জ্যা । বৃত্তের ওপর C যেকোনো একটি বিন্দু । O,A,C বিন্দুগামী বৃত্ত AQ জ্যা কে P বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে , CP = PQ
অঙ্কনঃ O,Q;O,C;C,Q যুক্ত করা হল ।
প্রমানঃ ∆OAQ এর
OA=OQ [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠OAQ = ∠OQA
বা, ∠PAO = ∠OQP —– (i)
আবার , O,A,C বিন্দুগামী বৃত্তের OP চাপের ওপর দুটি বৃত্তস্থ কোণ ∠OCP এবং ∠PAO
∴ ∠OCP=∠PAO —-(ii)
এখন , ∆OCQ এর
OC = OQ [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠OCQ = ∠OQC—-(iii)
অর্থাৎ , ∠OCP+∠PCQ=∠OQP+∠PQC—-(iv)
(i) নং ও(ii) নং সমীকরণ থেকে পাই ,
∠OQP=∠OCP—-(v)
(iv) ও (v) নং সম্পর্ক থেকে পাই ,
∴ ∠PCQ = ∠PQC
∴ ∆PCQ সমবাহু ত্রিভুজ
∴ CP=CQ [প্রমাণিত ]
9. একটি বৃত্তে ∆ABC ত্রিভুজটি অন্তর্লিখিত ।AX , BY এবং CZ যথাক্রমে ∠BAC , ∠ABC ও ∠ACB এর সমদ্বিখণ্ডক এবং যথাক্রমে X ,Y ,Z বিন্দুতে মিলিত হয় । প্রমান করি যে , AX , YZ- এর ওপর লম্ব ।

ত্রিভুজ ABC বৃত্তে অন্তর্লিখিত । AX ,BY এবং CZ যথাক্রমে BAC , ABC ও ACB এর সমদ্বিখণ্ডকত্রয় যথাক্রমে X,Y,Z বিন্দুতে মিলিত হয় ।ধরা হল AX এবং YZ পরস্পরকে P বিন্দুতে ছেদ করে । প্রমান করতে হবে যে , AX , YZ- এর ওপর লম্ব ।
অঙ্কনঃ X ,Y যুক্ত করা হল ।
প্রমানঃ AY চাপের ওপর অবস্থিত দুটি বৃত্তস্থ কোণ
∠AXY এবং ∠ABY
∴ ∠AXY =∠ABY —-(i)
আবার , BZ চাপের ওপর অবস্থিত দুটি বৃত্তস্থ কোণ
∠BYZ এবং ∠BCZ
∴∠BYZ = ∠BCZ —– (ii)
আবার , BX চাপের ওপর অবস্থিত দুটি বৃত্তস্থ কোণ
∠BYX এবং ∠BAX
∴ ∠BYX = ∠BAX —– (iii)
এখন, ∆PXY এর ,
∠PYX+∠PXY
=∠BYZ+∠BYX+∠AXY
=∠BCZ+∠BAX+∠ABY [ (i) ,(ii) ও(iii) নং সমীকরণে মাণ বসিয়ে পাই ]
= `\frac{1}{2}`∠BCA + `\frac{1}{2}`∠BAC + `\frac{1}{2}`∠ABC [∵AX , BY এবং CZ যথাক্রমে ∠BAC,∠ABC ও∠ACB এর সমদ্বিখণ্ডক]
= `\frac{1}{2}`✕( ∠BCA+∠BAC+∠ABC)
= `\frac{1}{2}`✕180°
= 90°
∴ ∠PYX+∠PXY =90°
∴ ∆PXY এর,
বহিঃস্থ কোণ ∠APY= বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টি
বা,∠APY= ∠PXY+∠PYX
বা,∠APY=90° [যেহেতু ,∠PXY+∠PYX=90°]
∴ AP ⊥ YZ
∴ AX , YZ এর ওপর লম্ব [প্রমাণিত]
10.একটি বৃত্তে ABC অন্তর্লিখিত । ∠BAC , ∠ABC ও ∠ACB এর সমদ্বিখণ্ডক বৃত্তে যথাক্রমে X ,Y ,Z বিন্দুতে মিলিত হয় ।প্রমান করি যে ∆XYZ এর ∠YXZ = 90 – `\frac{1}{2}`∠BAC
ABC একটি বৃত্তের অন্তর্লিখিত ত্রিভুজ। ∠A, ∠B, ∠C কোণের অন্তর্দ্বিখণ্ডক যথাক্রমে AX, BY, CZ.
AX, BY, CZ পরিধিকে যথাক্রমে X, Y, Z বিন্দুতে ছেদ করেছে। YZ, ZX, XY যুক্ত করা হল।

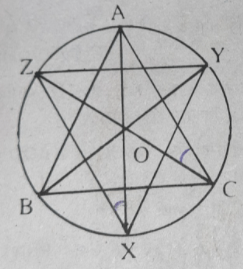
প্রমাণ করতে হবে XYZ ত্রিভুজের।
∠X= 90° –`\frac{A}{2}` , ∠Y = 90° – `\frac{B}{2}`, ∠Z=90° -`\frac{C}{2}`
প্রমাণ : একই চাপ AZ এর উপরিস্থ ∠AXZ ও ∠ACZ পরিধিস্থ কোণ।
∴ ∠AYZ = ∠ACZ = `\frac{1}{2}`∠C (∵ CZ, ∠C এর সমদ্বিখণ্ডক)। আবার, একই চাপ AY এর উপর দণ্ডায়মান ∠AXY ও ∠ABY পরিধিস্থ কোণ।
∴ ∠ABY = ∠AXY =`\frac{1}{2}`∠B.(∵ BY. ∠B এর সমদ্বিখণ্ডক)।
∴ ∠AXZ+ ∠AXY = `\frac{1}{2}`∠C +`\frac{1}{2}`∠B,∴ সমগ্র ∠X= `\frac{1}{2}` (∠B + ∠C) =`\frac{1}{2}` (180° – ∠A) = 90° -`\frac{A}{2}`
∴ ∠YXZ = 90 – `\frac{1}{2}`∠BAC [প্রমাণিত]
11.∆ABC এর A বিন্দু থেকে BC বাহুর উপর অঙ্কিত লম্ব BC বাহুকে D বিন্দুতে এবং B বিন্দু থেকে CA বাহুর ওপর অঙ্কিত লম্ব CA বাহুকে E বিন্দুতে ছেদ করে । প্রমান করি যে , A,B,D,E চারটি বিন্দু সমবৃত্তস্থ ।
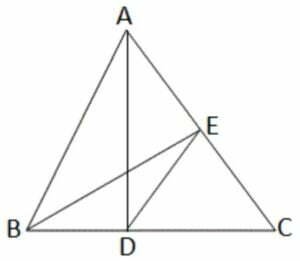
∆ABC এর A বিন্দু থেকে BC বাহুর উপর অঙ্কিত লম্ব BC বাহুকে D বিন্দুতে এবং B বিন্দু থেকে CA বাহুর ওপর অঙ্কিত লম্ব CA বাহুকে E বিন্দুতে ছেদ করে । প্রমান করতে হবে যে , A ,B,C ,D সমবৃত্তস্থ ।
অঙ্কনঃ D ,E যুক্ত করা হল ।
প্রমানঃ ∆EBC এবং ∆ADC থেকে পাই ,
∠BEC=∠ADC=1 সমকোণ
∠EDC সাধারণ কোণ
∴ অবশিষ্ট ∠EBC=অবশিষ্ট ∠DAC
অর্থাৎ , ∠EBC=∠DAE
যেহেতু , DE রেখাংশের একই পার্শ্বে অপর দুই বিন্দু B এবং A তে দুটি সমান কোণ উৎপন্ন করেছে , তাই A ,B,D ,E সমবৃত্তস্থ । [প্রমাণিত]
12. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(A)বহু বিকল্পীয় প্রশ্ন (M.C.Q):
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র ; ∠ACB = 30°, ∠ABC = 60°, ∠DAB = 35° এবং ∠DBC = x হলে , x এর মাণ
(a) 35°
(b) 70°
(c ) 65°
(d) 55°
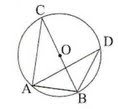
Ans: (d) 55°
সমাধানঃ ত্রিভুজ ∆ABC – তে ,
∠ACB+∠ABC+∠BAC=180°
বা, 30°+60°+∠BAC=180°
বা, ∠BAC = 90°
বা, ∠DAB+∠CAD = 90°
বা, 35°+∠CAD=90°
বা, ∠CAD= 55°
আবার , ∠CAD = ∠DBC [ ∵একই বৃত্তাংশস্থ সকল কোণের মাণ সমান ]
∴ ∠DBC = 55°
সুতরাং , x=55°
(ii) পাশের চিত্রে O বৃত্তের কেন্দ্র । ∠BAD = 65° , ∠BDC=45° হলে , ∠CBD এর মাণ
(a) 65°
(b) 45°
(c ) 40°
(d) 20°

Ans: (d) 20°
সমাধানঃ ∠BAD=65° এবং ∠BDC=45°
∴ ∠BAC =45° [ যেহেতু , ∠BDC=∠BAC (∵ একই বৃত্তাংশস্থ সকল কোণের মাণ সমান ) ]
∴ ∠CAD= ∠BAD- ∠BAC= 65°-45°=20°
আবার , ∠CAD = ∠CBD [ ∵একই বৃত্তাংশস্থ সকল কোণের মাণ সমান ]
∴ ∠CBD =20°
(iii) পাশের চিত্রে O বৃত্তের কেন্দ্র । ∠AEB = 110° এবং ∠CBE = 30° হলে , ∠ADB এর মাণ
(a) 70°
(b) 60°
(c ) 80°
(d) 90°
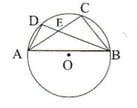
Ans: (C) 80°
বিকল্প পদ্ধতি
∠AEB = 110°
∴ ∠BEC = 180°-110°=70°
আবার , ∠CBE = 30°
∴ ABC এর , ∠ACB = 180°-(∠BEC+∠CBE)
=180°-(70°+30° )
=180°-100°
=80°
আবার , ∠ACB = ∠ADB= 80° [ ∵একই বৃত্তাংশস্থ সকল কোণের মাণ সমান ]
∴ ∠ADB = 80°
(iv) পাশের চিত্রে O বৃত্তের কেন্দ্র । ∠BCD = 28° , ∠AEC = 38° হলে ∠AXB এর মাণ
(a) 56°
(b) 86°
(c ) 38°
(d) 28°
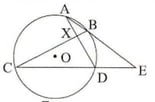
Ans: (b) 86°
সমাধানঃ
BD বৃত্তচাপের ওপর ∠BAD এবং ∠BCD একই বৃত্তাংশস্থ কোণ
আবার , ∠BCD = 28°
∴∠BCD=∠BAD = 28°
∴ ∠EAD=28°
∠AEC= 38°, ∴ ∠AED = 38° [একই কোণ ]
∠ADC=∠AED+∠DAE [ ∵ ত্রিভুজের বহিঃস্থ কোণের মাণ বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান ]
বা, ∠ADC= 38+28= 66°
আবার , ∠ADC= ∠ABC = 66° [ ∵ একই বৃত্তাংশস্থ সকল কোণের মাণ সমান ]
∴ ∠ABX=66 , ∠BAX = 28°
∠AXB
= 180°-(66°+28°)
=180°-94°
=86°
(v) পাশের চিত্রে O বৃত্তের কেন্দ্র এবংAB ব্যাস । AB ∥ CD , ∠ABC = 25° হলে , ∠CED এর মাণ
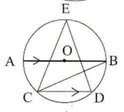
(a) 80°
(b) 50°
(c ) 25°
(d) 40°
Ans: (d) 40°
সমাধানঃ
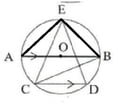
অঙ্কনঃ A, E; B,E যুক্ত করা হল ।
প্রমানঃ ∠AEB = 90° [ অর্ধবৃত্তস্থ কোণ সমকোণ ]
আবার,∠AEC= ∠ABC = 25° [ ∵ একই বৃত্তাংশস্থ সকল কোণের মাণ সমান ]
এবং,∠ABC = ∠BCD = 25° [∵ একান্তর কোণ ,AB||CD এবং CB ভেদক]
আবার , ∠BCD = ∠BED = 25°[ ∵ একই বৃত্তাংসস্থ সকল কোণের মাণ সমান ]
∴ ∠CED
= ∠AEB-(∠AEC+∠BED)
= 90°-(25°+25°)
=90°-50°
= 40°
∴ ∠CED = 40°
(B) সত্য বা মিথ্যা লিখি :
(i) পাশের চিত্রে AD ও BE যথাক্রমে ABC ত্রিভুজের BC ও AC বাহুর উপর লম্ব । A ,B,D,E বিন্দু চারটি সমবৃত্তস্থ ।
উত্তরঃ বিবৃতিটি সত্য ।
(ii) ABC ত্রিভুজের AB =AC ; BE ও CF যথাক্রমে ABC ও ACB এর সমদ্বিখণ্ডক এবং AC ও AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে । B ,C,E ,F বিন্দু চারটি সমবৃত্তস্থ নয় ।
উত্তরঃ বিবৃতিটি মিথ্যা ।
(C ) শূন্যস্থান পূরণ করিঃ
(i) একই বৃত্তাংশস্থ সকল কোণের মাণ ___________ ।
উত্তরঃ সমান
(ii) দুটি বিন্দুর সংযোজক সরলরেখাংশ তার একই পার্শ্বে অপর দুটি বিন্দুতে সমান সম্মুখ কোণ উৎপন্ন করলে বিন্দু চারটি __________ হবে ।
উত্তরঃ সমবৃত্তস্থ
(iii) একই বৃত্তে দুটি চাপ দ্বারা উৎপন্ন বৃত্তস্থ কোণ দুটি সমান হলে চাপ দুটির দৈর্ঘ্য _____________ ।
উত্তরঃ সমান
13. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A):
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র ,AC ব্যাস এবং জ্যা DE ও ব্যাস AC সমান্তরাল । ∠CBD =60° হলে , ∠CDE- এর মাণ নির্ণয় করি ।

সমাধানঃ

AB অঙ্কন করা হল ।
এখন ∠ABC = 90° [ ∵অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]
আবার , ∠CBD = 60°
∴ ∠ABD
= ∠ABC- ∠CBD
= 90°-60°
=30°
∠ABD = ∠ACD [ ∵একই বৃত্তাংশস্থ সকল কোণের মাণ সমান]
∴ ∠ACD = 30°
আবার , ∠ACD = ∠CDE [ একান্তর কোণ ]
∴ ∠CDE = 30° [উত্তর]
(ii) পাশের চিত্রে ∠PQR এর সমদ্বিখণ্ডক QS ; ∠SQR = 35° এবং ∠PRQ =32° হলে , ∠QSR এর মাণ নির্ণয় করি ।
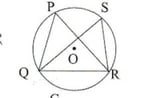
সমাধানঃ
∠PQR এর সমদ্বিখণ্ডক QS
∴ ∠PQS = ∠SQR
∠SQR = 35°
∴ ∠PQS =35°
আবার,∠PQR
=∠PQS+∠SQR
=35°+35°
=70°
এবং,∠QPR
= 180°-(∠PQR+∠PRQ)
= 180°-(70°+32°)
= 180°-102°
= 78°
আবার, ∠QPR = ∠QSR =78° [∵ একই বৃত্তস্থ সকল কোণের মাণ সমান ]
∴∠QSR =78°[উত্তর]
(iii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস । AB ও CD পরস্পর লম্ব এবং ∠ADC = 50° ; ∠CAD এর মাণ নির্ণয় করি ।

সমাধানঃ
AC বৃত্তচাপের ওপর ∠ABC এবং ∠ADC উভয়ই বৃত্তস্থ কোণ
∴ ∠ADC=∠ABC
∴ ∠ABC = 50°
আবার, ∠ACB = 90°[অর্ধবৃত্তস্থ কোণ] এবং ∠ABC = 50°
∴ ∠CAB = 180°-(90°+50°)=180°-140°=40°
∴ ∠BCD = 40° [ ∵AB ⊥ CD]
∠BCD=∠BAD [একই বৃত্তাংশস্থ কোণ]
∴ ∠BAD=40°[
∴ ∠CAD
=∠CAB+∠BAD
=40°+40°
=80°
∴ ∠CAD=80°[উত্তর]
(iv) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB=AC; ∠ABC=32° হলে , ∠BDC এর মাণ নির্ণয় করি ।
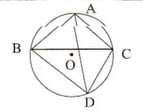
সমাধানঃ AB=AC এবং ∠ABC =32°
∴ ∠ACB = 32°
∴ ∠ADB=32° [∵ একই বৃত্তাংশস্থ সকল কোণের মাণ সমান ]
আবার , ∠ABC = 32 ∴∠ADC = 32° [ ∵একই বৃত্তাংশস্থ সকল কোণের মাণ সমান ]
∴ ∠BDC
=∠ADB+∠ADC
=32°+32°
=64°
∴ ∠BDC=64° [উত্তর]
(v) পাশের চিত্রে BX ও CY যথাক্রমে ∠ABC ও ∠ACB এর সমদ্বিখণ্ডক । AB=AC ও BY=4 সেমি. হলে, AX এর দৈর্ঘ্য নির্ণয় করি ।
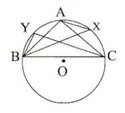
সমাধানঃ
AB=AC
∴ ∠ABC = ∠ACB
বা, ∠ABX+∠CBX=∠ACY+∠BCY
বা, ∠ABX+∠ABX=∠BCY+∠BCY [∵ BX ও CY যথাক্রমে ∠ ABC ও ∠ACB এর সমদ্বিখণ্ডক,∴∠ABX=∠CBX
আবার,∠BCY=∠ACY]
বা, 2∠ABX = 2∠BCY
বা, ∠ABX=∠BCY
∴ BY=AX=4 সেমি.
∴ AX=4 সেমি.[উত্তর]
Note: এই আর্টিকেলের ব্যাপারে তোমার মতামত জানাতে নীচে দেওয়া কমেন্ট বক্সে গিয়ে কমেন্ট করতে পারো। ধন্যবাদ।