Class 9 Mathematics Model Activity Task Part 8 Combined Answer 2021 | নবম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট ৮

প্রিয় ছাত্রছাত্রীরা, এই আর্টিকেলে আমরা নবম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট ৮ (Class 9 Mathematics Model Activity Task Part 8 Combined) এর সমস্ত প্রশ্ন ও উত্তর নিয়ে এসেছি । ২০২১ এর জুলাই থেকে অক্টোবর মাস পর্যন্ত যে সমস্ত মডেল অ্যাক্টিভিটি টাস্ক দেওয়া হয়েছিল সেখান থেকে বাছাই করা করা কিছু প্রশ্ন নিয়ে এবার তোমাদের কম্বাইন্ড অ্যাক্টিভিটি টাস্ক করতে দেওয়া হয়েছে ।

Class 9 Mathematics Model Activity Task Part 8 Combined

২০২১ এর এটাই সর্বশেষ অ্যাক্টিভিটি টাস্ক । এই অ্যাক্টিভিটি টাস্কে ৫০ নম্বরের প্রশ্ন দেওয়া রয়েছে যেগুলো তোমাদের সমাধান করে বিদ্যালয়ে জমা দিতে বলা হয়েছে । এর উপর ভিত্তি করেই সম্ভাবত তোমরা পরবর্তী শ্রেণীতে উত্তীর্ণ হবে । সুতরাং, খুবই মন দিয়ে তোমরা নিচের প্রশ্নোত্তর গুলি পড়বে এবং লিখবে ।

মডেল অ্যাক্টিভিটি টাস্ক Part 8 (Combined), October 2021

গণিত (পূর্ণমান ৫০)

নবম শ্রেণী

Class 9 Mathematics Model Activity Task Part 8 Solution :

নীচের প্রশ্নগুলির উত্তর লেখাে : 

1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs) :

(i) একজন সবজি বিক্রেতা 20 টাকায় 10 টি লেবু কিনে 20 টাকায় ৪টি লেবু বিক্রি করেন, তার শতকরা লাভ হয় 

(a) 25

(b) 20 

(c) 10

(d) 24 

উত্তর: (a) 25

ব্যাখ্যা: 10 টি লেবুর ক্রয়মুল্য 20 টাকা

1 টি লেবুর ক্রয়মুল্য `\frac20{10}` = 2 টাকা

আবার 8 টি লেবুর ক্রয়মুল্য 20 টাকা

∴ 1 টি লেবুর ক্রয়মুল্য `\frac20{8}` = `\frac5{2}` = 2.5 টাকা

∴ লাভ = (2.5-2) = .5 টাকা

∴ শতকরা লাভ = × 100% = `\frac{\cancel\cdot5}{\cancel2}` × `\frac{\overset5{\cancel{10}}\cancel0\%}{1\cancel0}` = 25 টাকা

(ii) P Q R S ট্রাপিজিয়ামের দুটি তির্যক বাহু PS ও QR-এর মধ্যবিন্দু যথাক্রমে X ও Y, তবে XY = 

(a) `\frac1{2}` PQ

(b) `\frac1{2}` RS 

(c) `\frac1{2}` (PQ+RS)

(d) `\frac1{2}` (PQ-RS) 

উত্তর: (c) `\frac1{2}` (PQ+RS)

(iii) 105 – 140 শ্রেণিটির পরিসংখ্যা 14 হলে, শ্রেণিটির পরিসংখ্যা ঘনত্ব হবে 

(a) 2.5

(b) 0.4 

(c) 0.35

(d) 0.14 

উত্তর: (b) 0.4

ব্যাখ্যা: 105 – 140 শ্রেণিটির শ্রেণি দৈর্ঘ্য = 140 – 105 = 35 এবং পরিসংখ্যা = 14

∴ শ্রেণিটির পরিসংখ্যা ঘনত্ব = পরিসংখ্যা/দৈর্ঘ্য = `\frac{\overset2{\cancel{14}}}{\underset5{\cancel{35}}}` = `\frac2{5}` = 0.4

(iv) 3 মিটার লম্বা ও 2 মিটার চওড়া একটি আয়তাকার জায়গা 5 ডেসিমি. বর্গ টালি দিয়ে বাঁধাতে হলে টালি লাগবে 

(a) 48 টি

(b) 96 টি 

(c) 24 টি

(d) 72 টি 

উত্তর: (c) 24 টি

ব্যাখ্যা: আয়তাকার জায়গার ক্ষেত্রফল = 3 মিটার × 2 মিটার = 30 ডেসিমিটার × 20 ডেসিমিটার = 600 বর্গ ডেসিমিটার

∴ টালির ক্ষেত্রফল = 5 × 5 বর্গ ডেসিমিটার = 25 বর্গ ডেসিমিটার

∴ টালির সংখ্যা = `\frac{\overset{\overset{24}{\cancel{120}}}{\cancel{600}}}{\underset{\cancel5}{\cancel{25}}}` = 24 টি

(v) শতকরা লাভ 10 হলে, ক্রয়মূল্য ও বিক্রয়মূল্যের অনুপাত হবে 

(a) 1:10

(b) 10:1 

(c) 10:11

(d) 11:10

উত্তর: (c) 10:11

ব্যাখ্যা: শতকরা লাভ = 10

∴ মোট লাভ/ক্রয়মূল্য × 100 = 10

বা, লাভ/ক্রয়মূল্য = `\frac10{100}` = `\frac1{10}` = x (ধরি)

∴ লাভ = x এবং ক্রয়মূল্য = 10x

∴ বিক্রয়মূল্য = ক্রয়মূল্য + লাভ = 10x + x = 11x

∴ ক্রয়মূল্য : বিক্রয়মূল্য = 10x : 11x = 10:11

(vi) Δ ABC-এর AB বাহুর মধ্যবিন্দু D দিয়ে BC-এর সমান্তরাল DE টানা হলাে যা AC বাহুকে E বিন্দুতে ছেদ করলাে,

তাহলে 

(a) AE = `\frac1{3}` AC

(b) AE = `\frac1{2}` AC 

(c) AE= `\frac1{4}` AC

(d) AE = `\frac2{3}` AC

উত্তর: (b) AE = `\frac1{2}` AC 

(vii) যে অর্ধবৃত্তাকার চাকতির ব্যাসার্ধের দৈর্ঘ্য 10.5 সেমি. তার পরিসীমা হলাে

(a) 2π x 10.5 সেমি.

(b) (π + 2) x 10.5 সেমি. 

(c) 2(π + 1) x 10.5 সেমি.

(d) (π + 1) x 10.5 সেমি.

উত্তর: (b) (π + 2) x 10.5 সেমি. 

ব্যাখ্যা: অর্ধবৃত্তাকার চাকতির পরিসীমা

= `\frac{2πr}{2}` + 2r সেমি.

= πr + 2r সেমি.

= (π + 2) × r সেমি.

= (π + 2) × 10.5 সেমি.

(viii) যে বর্গাকার চিত্রে কর্ণের দৈর্ঘ্য সেমি., তার একটি বাহুর দৈর্ঘ্য হবে

(a) `\frac{13\sqrt2}2` সেমি.

(b) 26 সেমি. 

(c) `\sqrt338`সেমি.

(d) 13 সেমি.

উত্তর: (d) 13 সেমি.

ব্যাখ্যা: বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য =`\sqrt2` × বাহু একক

অতএব, `\sqrt2` × বাহু = 13`\sqrt2`

বা, বাহু = 13

2. সত্য/মিথ্যা (T/F) লেখাে :

(i) ABC সমকোণী ত্রিভুজের ∠BAC= 90° এবং BC-এর মধ্যবিন্দু D হলে, AD= `\frac1{2}`BC

উত্তর: সত্য

(ii) একটি পরিসংখ্যা বিভাজন তালিকায় একটি শ্রেণির মধ্যবিন্দু 10 এবং প্রতিটি শ্রেণির শ্রেণি-দৈর্ঘ্য 6 হলে, শ্রেণিটির নিম্নসীমা হবে 8।

উত্তর: মিথ্যা

ব্যাখ্যা: ধরি, শ্রেনিটির উচ্চসীমা = H এবং নিম্নসীমা = L

∵ শ্রেনিটির মধ্যবিন্দু = 10

∴ `\frac{H+L}{2}` = 10 => H + L = 20 —(i)

আবার শ্রেনিটির শ্রেণি-দৈর্ঘ্য = 6

∴ H – L = 6 —(ii)

∴ (i)-(ii) করে পাই, 2L = 20 – 6

বা, 2L = 14

বা, L = `\frac14{2}`

∴ L = 7

(iii) একটি সামান্তরিক আকারের ক্ষেত্র, একটি আয়তক্ষেত্র এবং একটি ত্রিভুজাকার ক্ষেত্র একই ভূমি ও একই সমান্তরাল সরলরেখা যুগলের মধ্যে অবস্থিত এবং তাদের ক্ষেত্রফল যথাক্রমে P, R ও T হলে P = R = `\frac{T}{2}` হবে। 

উত্তর: মিথ্যা

(iv) একটি সমবাহু ত্রিভুজের ক্ষেত্রফল ও উচ্চতার সাংখ্যমান সমান হলে, ত্রিভুজটির বাহুর দৈর্ঘ্য হবে 1 একক। 

উত্তর: মিথ্যা

ব্যাখ্যা: সমবাহু ত্রিভূজের ক্ষেত্রফল = `\sqrt{\frac3{4}}` × (বাহু)² বর্গ একক এবং উচ্চতা = `\sqrt{\frac3{2}}` × বাহু একক

∴ প্রশ্নানুসারে, `\sqrt{\frac3{4}}` × (বাহু)² = `\sqrt{\frac3{2}}` × বাহু একক

বা, বাহু = `\frac4{2}` = 2

(v) ধার্যমূল্যের উপর ছাড় নির্ভর করে। 

উত্তর: সত্য

(vi) পরিসংখ্যা বহুভুজ অঙ্কনের জন্য প্রথম শ্রেণির ঠিক আগের একটি শ্রেণির পরিসংখ্যা হবে ‘0’

উত্তর: সত্য

(vii) 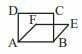চিত্রে, ABCD বর্গক্ষেত্রের ক্ষেত্রফল ABEF রসম্ব আকার ক্ষেত্রের ক্ষেত্রফলের সমান।

উত্তর: মিথ্যা

(viii) প্রতিটি বৃত্তের পরিধি ও ব্যাসের দৈর্ঘ্যের অনুপাত একটি নির্দিষ্ট সংখ্যা। 

উত্তর: সত্য

ব্যাখ্যা: মনে করি, বৃত্তের ব্যাসার্ধ = r একক

∴ বৃত্তের ব্যাস = 2r একক

এবং বৃত্তের পরিধি = 2πr একক

∴ বৃত্তের পরিধি : ব্যাস = 2πr : 2r = π : 1

অর্থ্যাৎ, বৃত্তের পরিধি ও ব্যাসের দৈর্ঘ্যের অনুপাত সর্বদা π হবে যা একটি নির্দিষ্ট সংখ্যা।

3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.):

(i) g(x) = 2x – 16 বহুপদী সংখ্যামালাটির সমীকরণটি লেখাে এবং বহুপদী সংখ্যামালাটির শূন্য নির্ণয় করাে। 

উত্তর: g(x) = 2x – 16 বহুপদী সংখ্যমালার সমীকরণটি হলো, g(x) = 0

অর্থ্যাৎ, 2x – 16 = 0

∴ 2x = 16

বা, x = 8

সুতরাং, x = 8 এর জন্য g(x) এর মান শুন্য হবে।

(ii) (8x³ + 8x – 5) বহুপদী সংখ্যামালাটির একটি উৎপাদক নির্ণয় করাে। 

উত্তর: `8x^3+8x-5`

`=8x^3-1+8x-4`

`=(2x)^3-(1)^3+4(2x-1)`

`=(2x-1)(4x^2+2x+1)+4(2x-1)`

`=(2x-1)(4x^2+2x+1+4)`

`=(2x-1)(4x^2+2x+5)`

∴ `8x^3+8x-5` বহুপদী সংখ্যামালাটির একটি উৎপাদক `(2x-1)` অথবা `4x^2+2x+5`

(iii) (-2, -2) এবং (4, 6) বিন্দু দুটির মধ্যে দূরত্ব নির্ণয় করাে। 

উত্তর: (-2, -2) এবং (4, 6) বিন্দু দুটির মধ্যে দূরত্ব

`=\sqrt{(4+2)^2+(6+2)^2}` একক

`=\sqrt{(6)^2+(8)^2}` একক

`=\sqrt{36+64}` একক

`=\sqrt{100}` একক

= 10 একক

(iv) একটি ঘড়ি পরপর 10% ও 5% ছাড়ে বিক্রয় করা হলে সমতুল্য ছাড় কত হবে? 

উত্তর: ধরি, ঘড়িটির ধার্য্য মূল্য = 100 টাকা

10% ছাড় দিলে ছাড়ের পরিমাণ হবে = 10 টাকা

∴ প্রথম ছাড়ে ঘড়িটির মূল্য হবে = 100-10 = 90 টাকা

দ্বিতীয় বার ছাড় দেওয়া হবে এই 90 টাকার উপর

∴ 90 টাকার উপর 5% ছাড় দিলে ছাড়ের পরিমাণ হবে

= 90 × 5% = `9\cancel0\times\frac{\cancel5}{\underset2{\cancel{10}}\cancel0}` = `\frac9{2}` = 4.5 টাকা

∴ সর্বমোট ছাড়ের পরিমাণ = (10+4.5) = 14.5 টাকা

∴ সর্বমোট ছাড় = `\frac{14.5}{100}\times100\%` = 14.5%

(v) একটি বৃত্তের ব্যাসের দৈর্ঘ্য এবং একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য সমান হলে, তাদের পরিসীমার অনুপাত কত হবে? 

উত্তর: মনে করি, বৃত্তের ব্যাসার্ধ = r একক

∴ বৃত্তের ব্যাস = 2r একক

আবার মনে করি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = a একক

∴ বর্গক্ষেত্রের পরিসীমা = 4a একক

প্রশ্নানুসারে, 2r = a

∴ বৃত্তের পরিসীমা : বর্গক্ষেত্রের পরিসীমা

= 2πr : 4a

= 2πr : 4×2r

= π : 4

= `\frac22{7}` : 4

= 22 : 4×7

= 11:14

(vi) 10টি পেনের ক্রয়মূল্য ৪টি পেনের বিক্রয়মূল্যের সমান হলে, শতকরা লাভ নির্ণয় করাে।

উত্তর: মনে করি, প্রতিটি পেনের ক্রয়মূল্য = `x` টাকা

∴ 10 টি পেনের ক্রয়মূল্য = `10x` টাকা

∴ 8 টি পেনের বিক্রয়মূল্য = `10x` টাকা

∴ 1 টি পেনের বিক্রয়মূল্য = `\frac{10x}{8}` টাকা

∴ x টাকার লাভ = `\frac{5x}{4}-x` টাকা = `\frac{x}{4}` টাকা

∴ শতকরা লাভ = লাভ/ক্রয়মূল্য × 100

= `\frac{\frac x4}x\times100`

= `\frac1{4}\times100`

= 25 টাকা

(vii) 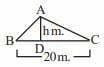চিত্রে, ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 96 বর্গমি. এবং ভূমি BC = 20 মি. হলে, ত্রিভুজটির উচ্চতা h মি. নির্ণয় করাে।

উত্তর: আমরা জানি, ত্রিভুজের ক্ষেত্রফল = `\frac1{2}` × ভুমি × উচ্চতা

বা, 96 = `\frac1{2}` × 20 × h

বা, h = `\frac{96\times\cancel2}{\underset{10}{\cancel{20}}}`

বা, h = 9.6

∴ ত্রিভুজটির উচ্চতা 9.6 মিটার।

4. (i) যুক্তি দিয়ে প্রমাণ করাে, যে-কোনাে চতুর্ভুজের একজোড়া বিপরীতবাহু সমান ও সমান্তরাল হলে, চতুর্ভুজটি সামান্তরিক হবে। 

উত্তর:

(ii) যুক্তি দিয়ে প্রমাণ করাে যে, কোনাে ত্রিভুজের দুটি বাহুর মধ্যবিন্দুদ্বয়ের সংযােজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক।

উত্তর:

(ii) সমদ্বিবাহু ত্রিভুজ অঙ্কন করাে যার সমান বাহু দুটির প্রত্যেকটির দৈর্ঘ্য ৪ সেমি. এবং সমান বাহু দুটির অন্তর্ভুক্ত কোণ 30°; ওই ত্রিভুজটির সমান ক্ষেত্রফলবিশিষ্ট একটি আয়তক্ষেত্র অঙ্কন করাে (কেবলমাত্র অঙ্কন চিহ্ন দিতে হবে)। 

উত্তর:

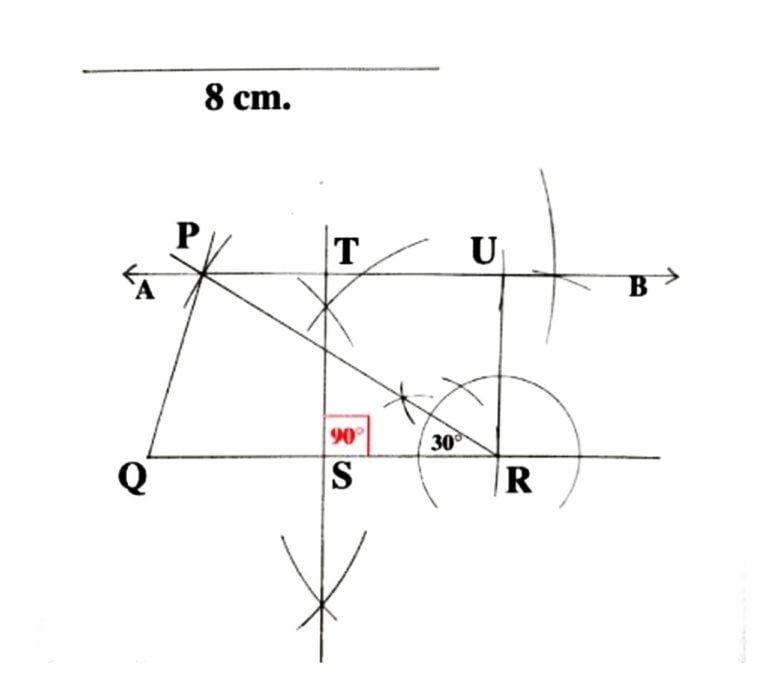
PQR একটি সমদ্বিবাহু ত্রিভুজ অঙ্কন করলাম যার সমান বাহু দুটি হলো PR = QR = 8 সেমি. এবং সমান বাহু দুটির অন্তর্ভুক্ত কোণ ∠SRU = 30° | এই PQR সমদ্বিবাহু ত্রিভুজের সমান ক্ষেত্রফলবিশিষ্ট একটি আয়তক্ষেত্র RSTU অঙ্কনকরা হলো |

(iv) নীচের পরিসংখ্যা বিভাজন ছকটির পরিসংখ্যা বহুভুজ অঙ্কন করাে।

উত্তর:

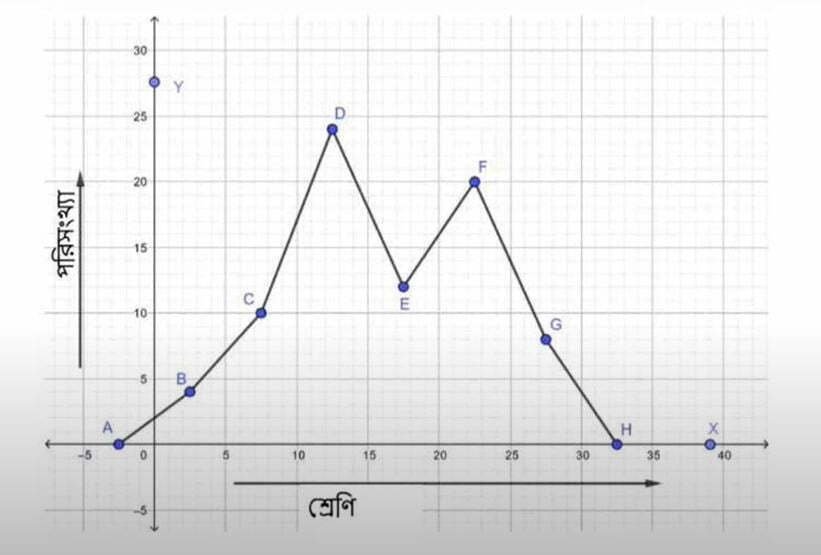
x-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহু = 1 একক এবং y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহু = 1 একক ধরলাম। 

এরপর ছক কাগজে (-2.5,0), (2.5,4), (7.5,10), (12.5,24), (17.5,12), (22.5,20), (27.5,4), (32.5,0) বিন্দুগুলি পরপর সরলরেখাংশ দ্বারা যােগ করে ABCDEFGH পরিসংখ্যা বহুভুজটি অঙ্কন করলাম।

Read Also:

Class 9 English 2nd Language Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 9 Bengali (বাংলা প্রথম ভাষা) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 9 History (ইতিহাস) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 9 Geography (ভূগোল) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 9 Life Science (জীবন বিজ্ঞান) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 9 Physical Science (ভৌতবিজ্ঞান) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8

Class 1-10 Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8