প্রিয় ছাত্রছাত্রীরা এই আর্টিকেলে আমরা Koshe Dekhi 1.3 Class 6 Solution নিয়ে এসেছি। তোমাদের ষষ্ঠ শ্রেণির গণিতপ্রভা পাঠ্যবইতে কষে দেখি 1.3 থেকে কিছু ভগ্নাংশের অঙ্ক রয়েছে। সেগুলির খুবই সহজ সমাধান আমরা এখান করে দিলাম। আশা করি সবার ভালো লাগবে।
কষে দেখি 1.3 – ষষ্ঠ শ্রেণি
পূর্বপাঠের পুনরালোচনা – ভগ্নাংশ
Koshe Dekhi 1.3 Class 6 Solution | গণিতপ্রভা | ষষ্ঠ শ্রেণি
1. ফাঁকা ঘরে লিখি –
(a)
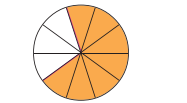
উত্তর: $\frac{7}{10}$ অংশ রং করা।
(b)
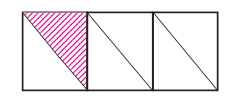
উত্তর: $\frac{5}{6}$ অংশ রং করা।
(c) $\frac{2}{5}$ অংশ রং করি।
উত্তর:

2. মনে মনে ভেবে নিজে করি –
(a) অর্ধেক রুটি বলতে মোট রুটির কত অংশ দেখি।
উত্তর: অর্ধেক রুটি বলতে মোট রুটির $\frac{1}{2}$ অংশ।
(b) আমার কাছে একটি বড়ো চকোলেট আছে। আমি সেই চকোলেটকে সমান 8টি টুকরো করে তার 3টি টুকরো বোনকে, 2টি টুকরো ভাইকে দিলাম ও বাকি টুকরোগুলি নিজে খেলাম। আমরা কে কে চকোলেটের কত অংশ পেলাম দেখি ।
সমাধান:
মোট চকলেটকে সমান 8 টি টুকরো করলাম।
বোনকে দিয়েছি 3 টি টুকরো = $\frac{3}{8}$ অংশ।
ভাইকে দিয়েছি 2 টি টুকরো = $\frac{2}{8}$ অংশ।
∴ ভাই ও বোনকে মোট দিয়েছি $(\frac{3}{8}$ + $\frac{2}{8})$ অংশ
= $\frac{3 + 2}{8}$ = $\frac{5}{8}$ অংশ।
মোট অংশ = 1 অংশ
∴ আমি পেলাম = (1 – $\frac{5}{8}$) অংশ
= $\frac{8 – 5}{8}$ = $\frac{3}{8}$ অংশ
∴ বোন পেল = $\frac{3}{8}$ অংশ, ভাই পেল = $\frac{2}{8}$ অংশ এবং আমি পেলাম $\frac{3}{8}$ অংশ। (উত্তর:)
(c) 1 থেকে 10 পর্যন্ত পূর্ণসংখ্যাগুলি ও মৌলিক সংখ্যাগুলি লিখি। এদের মধ্যে মোট পূর্ণ সংখ্যার কত অংশ মৌলিক সংখ্যা আছে খুঁজি।
সমাধান:
1 থেকে 10 পর্যন্ত পূর্ণসংখ্যা = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 = 10 টি
এবং 1 থেকে 10 এর মধ্যে মৌলিক সংখ্যা = 2, 3, 5, 7 = 4 টি
∴ মোট $\frac{4}{10}$ অংশ মৌলিক সংখ্যা।
আবার, $\frac{4}{10}$ = $\frac{2}{5}$ অংশ মৌলিক সংখ্যা।
∴ 1 থেকে 10 পর্যন্ত মোট পূর্ণ সংখ্যার $\frac{2}{5}$ অংশ মৌলিক সংখ্যা আছে। ∴ বোন পেল = $\frac{3}{8}$ অংশ, ভাই পেল = $\frac{2}{8}$ অংশ এবং আমি পেলাম $\frac{3}{8}$ অংশ। (উত্তর:)
(d) ঝুড়িতে কিছু কমলালেবু আছে। অর্ধেক লেবু দাদুকে দেওয়ার পরে ঝুড়িতে 2টি লেবু পড়ে রইল। দাদুকে দেওয়ার আগে ঝুড়িতে কটি লেবু ছিল হিসাব করি।
সমাধান:
অর্ধেক লেবু দাদুকে দেওয়ার পরে ঝুড়িতে 2 টি লেবু পড়ে রইল।
মোট লেবু = 1 অংশ
অর্ধেক লেবু = $\frac{1}{2}$ অংশ
∴ $\frac{1}{2}$ + $\frac{1}{2}$ = $\frac{1 + 1}{2}$ = $\frac{2}{2}$ = 1 অংশ
অর্ধেক = 2 টি লেবু
∴ মোট লেবু = 2 + 2 = 4 টি লেবু
∴ দাদুকে দেওয়ার আগে ঝুড়িতে 4 টি লেবু ছিল। (উত্তর:)
(e) একই মাপের দুটি গ্লাসে একই পরিমাণ সরবত তৈরি করা হলো। প্রথম গ্লাসের সরবতের $\frac{1}{5}$ অংশ চিনি আছে, দ্বিতীয় গ্লাসের সরবতে $\frac{2}{7}$ অংশ চিনি আছে। সরবত খাওয়ার আগেই কোন গ্লাসের সরবত বেশি মিষ্টি দেখি।
সমাধান:
প্রথম গ্লাসে চিনি আছে $\frac{1}{5}$ অংশ
দ্বিতীয় গ্লাসে চিনি আছে $\frac{2}{7}$ অংশ
∴ $\frac{1}{5}$ ও $\frac{2}{7}$ ভগ্নাংশ দুটিকে তুলনা করে পাই,
$\frac{1}{5}$ = $\frac{1 × 7}{5 × 7}$ = $\frac{7}{35}$
$\frac{2}{7}$ = $\frac{2 × 5}{7 × 5}$ = $\frac{10}{35}$
যেহেতু, $\frac{10}{35} > \frac{7}{35}$
অর্থাৎ, $\frac{2}{7} > \frac{1}{5}$
∴ দ্বিতীয় গ্লাসের সরবতে বেশি মিষ্টি আছে। (উত্তর:)
(f) স্কুলের গেটে $\frac{5}{7}$ অংশ রং করা হয়ে গেছে। কত অংশ রং করতে এখনো বাকি আছে হিসাব করি।
সমাধান:
মোট অংশ = 1 অংশ
রং করা হয়েছে = $\frac{5}{7}$ অংশ
∴ বাকি আছে = 1 – $\frac{5}{7}$
= $\frac{7 – 5}{7}$ = $\frac{2}{7}$ অংশ
∴ রং করতে এখনও বাকি আছে $\frac{2}{7}$ অংশ। (উত্তর:)
(g) আমার কাছে 20 টাকা আছে। আমি 5 টাকা খরচ করলাম। আমি আমার টাকার কত অংশ খরচ করলাম ও কত অংশ এখনও আমার কাছে হিসাব করি।
সমাধান:
মোট টাকা = 20 টাকা
খরচ করেছি = 5 টাকা
∴ খরচ করেছি $\frac{5}{20}$ অংশ = $\frac{1}{4}$ অংশ
মোট অংশ = 1 অংশ
∴ বাকি আছে 1 – $\frac{1}{4}$ অংশ
= $\frac{4 – 1}{4}$ অংশ
= $\frac{3}{4}$ অংশ
∴ আমি আমার টাকার $\frac{1}{4}$ অংশ খরচ করলাম ও $\frac{3}{4}$ অংশ এখনও আমার কাছে আছে। (উত্তর:)
(h) রাজিয়ার কাছে 36টি কুল আছে। সে তার মোট কুলের $\frac{2}{3}$ অংশ আমাকে দেবে। রাজিয়া কতগুলি কুল আমাকে দেবে হিসাব করি।
সমাধান:
মোট কুল = 36 টি এবং রাজিয়া আমাকে দেবে $\frac{2}{3}$ অংশ
∴ আমাকে দেবে $\overset{12}{\cancel{36}}$ × $\frac{2}{\cancel3}$ টি = 24 টি
= 12 × 2 টি
= 24 টি
∴ রাজিয়া আমাকে মোট 24 টি কুল দেবে। (উত্তর:)
3. ভগ্নাংশগুলি ছবির সাহায্যে দেখাই –
(a) $\frac{1}{5}$
উত্তর:
(b) $\frac{3}{8}$
উত্তর:
(c) $\frac{14}{5}$
উত্তর:
$\frac{14}{5}$ = $2\frac{4}{5}$
∴ চিত্রটি হবে
(d) $2\frac{3}{7}$
উত্তর:
(e) $\frac{8}{5}$
উত্তর:
$\frac{8}{5}$ = $1\frac{3}{5}$
∴ চিত্রটি হবে
(f) $\frac{11}{7}$
উত্তর:
$\frac{11}{7}$ = $1\frac{4}{7}$
∴ চিত্রটি হবে
4. প্রকৃত ভগ্নাংশে ◯, অপ্রকৃত ভগ্নাংশে ▢ ও মিশ্র ভগ্নাংশে △ বসাই –

উত্তর:
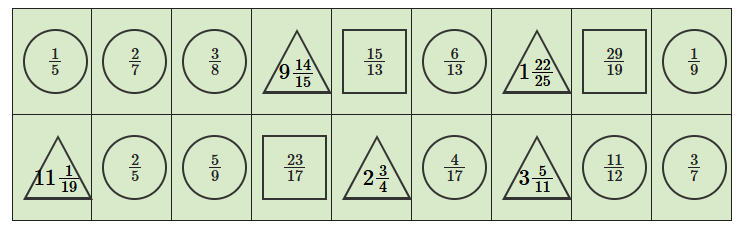
5. নীচের প্রতিটি ভগ্নাংশের তিনটি সমতুল্য ভগ্নাংশ লিখি –
(a) $\frac{1}{5}$
উত্তর:
$\frac{1}{5}$ এর তিনটি সমতুল্য ভগ্নাংশ তিনটি হল –
$\frac{1 × 2}{5 × 2} = \frac{2}{10}$
$\frac{1 × 3}{5 × 3} = \frac{3}{15}$
$\frac{1 × 4}{5 × 4} = \frac{4}{20}$
(b) $\frac{2}{5}$
উত্তর:
$\frac{2}{5}$ এর তিনটি সমতুল্য ভগ্নাংশ তিনটি হল –
$\frac{2 × 2}{5 × 2} = \frac{4}{10}$
$\frac{2 × 3}{5 × 3} = \frac{6}{15}$
$\frac{2 × 4}{5 × 4} = \frac{8}{20}$
(c) $1\frac{1}{3}$
উত্তর:
$1\frac{1}{3}$ বা $\frac{4}{3}$ এর তিনটি সমতুল্য ভগ্নাংশ তিনটি হল –
$\frac{4 × 2}{3 × 2} = \frac{8}{6}$ (বা $1\frac{2}{6}$)
$\frac{4 × 3}{3 × 3} = \frac{12}{9}$ (বা $1\frac{3}{9}$)
$\frac{4 × 4}{3 × 4} = \frac{16}{12}$ (বা $1\frac{4}{12}$)
(d) $6\frac{1}{6}$
উত্তর:
$6\frac{1}{6}$ বা $\frac{37}{6}$ এর তিনটি সমতুল্য ভগ্নাংশ তিনটি হল –
$\frac{37 × 2}{6 × 2} = \frac{74}{12}$ (বা $6\frac{2}{12}$)
$\frac{37 × 3}{6 × 3} = \frac{111}{18}$ (বা $6\frac{3}{18}$)
$\frac{37 × 4}{6 × 4} = \frac{148}{24}$ (বা $6\frac{4}{24}$)
(e) $3\frac{4}{5}$
উত্তর:
$3\frac{4}{5}$ বা $\frac{19}{5}$ এর তিনটি সমতুল্য ভগ্নাংশ তিনটি হল –
$\frac{19 × 2}{5 × 2} = \frac{38}{10}$ (বা $3\frac{8}{10}$)
$\frac{19 × 3}{5 × 3} = \frac{57}{15}$ (বা $3\frac{12}{15}$)
$\frac{19 × 4}{5 × 4} = \frac{76}{20}$ (বা $3\frac{16}{20}$)
6. নীচের ভগ্নাংশগুলিকে লঘিষ্ঠ আকারে প্রকাশ করি —
(a) $\frac{28}{49}$
সমাধানঃ
| 4 | |
| $\cancel{28}$ | |
| $\cancel{49}$ | |
| 7 |
= $\frac{4}{7}$ (উত্তর:)
(b) $\frac{54}{81}$
সমাধানঃ
| 2 | |||
| $\cancel{6}$ | |||
| $\cancel{18}$ | |||
| $\cancel{54}$ | |||
| $\cancel{81}$ | |||
| $\cancel{27}$ | |||
| $\cancel{9}$ | |||
| 3 |
= $\frac{2}{3}$ (উত্তর:)
(c) $\frac{72}{108}$
সমাধানঃ
| 2 | |||
| $\cancel{8}$ | |||
| $\cancel{24}$ | |||
| $\cancel{72}$ | |||
| $\cancel{108}$ | |||
| $\cancel{36}$ | |||
| $\cancel{12}$ | |||
| 3 |
= $\frac{2}{3}$ (উত্তর:)
(d) $\frac{243}{405}$
সমাধানঃ
| 3 | |||
| $\cancel{27}$ | |||
| $\cancel{81}$ | |||
| $\cancel{243}$ | |||
| $\cancel{405}$ | |||
| $\cancel{135}$ | |||
| $\cancel{45}$ | |||
| 5 |
= $\frac{3}{5}$ (উত্তর:)
(e) $\frac{165}{180}$
সমাধানঃ
| 11 | ||
| $\cancel{33}$ | ||
| $\cancel{165}$ | ||
| $\cancel{180}$ | ||
| $\cancel{36}$ | ||
| 12 |
= $\frac{11}{12}$ (উত্তর:)
7. নীচের ভগ্নাংশগুলি ছোটো থেকে বড়ো (ঊর্ধ্বক্রমে) সাজাই –

(a) $\frac{7}{2}, \frac{7}{4}, \frac{7}{5}$
সমাধানঃ
হরগুলির ল.সা.গু. করে পাই –
| 2 | 2, | 4, | 5 |
| 1, | 2, | 5 |
ল.সা.গু. = 2 × 1 × 2 × 5 = 20
$\frac{7}{2}$ = $\frac{7 × 10}{2 × 10}$ = $\frac{70}{20}$
$\frac{7}{4}$ = $\frac{7 × 5}{4 × 5}$ = $\frac{35}{20}$
$\frac{7}{5}$ = $\frac{7 × 4}{5 × 4}$ = $\frac{28}{20}$
∴ ছোটো থেকে বড়ো হিসেবে সাজালে পাই = $\frac{7}{5}, \frac{7}{4}, \frac{7}{2}$ (উত্তর:)
(b) $5\frac{3}{4}, 5\frac{5}{9}, 5\frac{8}{12}$
সমাধানঃ
এখানে ভগ্নাংশগুলো হলো: $5\frac{3}{4}$ = $\frac{23}{4}$, $5\frac{5}{9}$ = $\frac{50}{9}$ এবং $5\frac{8}{12}$ = $\frac{68}{12}$
হরগুলির ল.সা.গু. করে পাই –
| 2 | 4, | 9, | 12 |
| 2 | 2, | 9, | 6 |
| 3 | 1, | 9, | 3 |
| 1, | 3, | 1 |
ল.সা.গু. = 2 × 2 × 3 × 1 × 3 × 1 = 36
$5\frac{3}{4}$ = $\frac{23}{4}$ = $\frac{23 × 9}{4 × 9}$ = $\frac{207}{36}$
$5\frac{5}{9}$ = $\frac{50}{9}$ = $\frac{50 × 4}{9 × 4}$ = $\frac{200}{36}$
$5\frac{8}{12}$ = $\frac{68}{12}$ = $\frac{68 × 3}{12 × 3}$ = $\frac{204}{36}$
∴ ছোট থেকে বড় হিসেবে সাজালে পাই $= \frac{50}{9}, \frac{68}{12}, \frac{23}{4}$ অর্থাৎ, $5\frac{5}{9}, 5\frac{8}{12}, 5\frac{3}{4}$ (উত্তর:)
(c) $1\frac{1}{5}, 1\frac{1}{7}, 1\frac{1}{8}$
সমাধানঃ
এখানে ভগ্নাংশগুলো হলো: $1\frac{1}{5} = \frac{6}{5}$, $1\frac{1}{7} = \frac{8}{7}$ এবং $1\frac{1}{8} = \frac{9}{8}$
হরগুলির ল.সা.গু. করে পাই –
(যেহেতু সংখ্যাগুলোর মধ্যে কোনো সাধারণ উৎপাদক নেই)
∴ ল.সা.গু. = 5 × 7 × 8 = 280
$1\frac{1}{5}$ = $\frac{6}{5}$ = $\frac{6 × 56}{5 × 56}$ = $\frac{336}{280}$
$1\frac{1}{7}$ = $\frac{8}{7}$ = $\frac{8 × 40}{7 × 40}$ = $\frac{320}{280}$
$1\frac{1}{8}$ = $\frac{9}{8}$ = $\frac{9 × 35}{8 × 35}$ = $\frac{315}{280}$
∴ ছোট থেকে বড় হিসেবে সাজালে পাই = $\frac{9}{8}, \frac{8}{7}, \frac{6}{5}$ অর্থাৎ, $1\frac{1}{8}, 1\frac{1}{7}, 1\frac{1}{5}$ (উত্তর:)
(d) $\frac{1}{3}, \frac{4}{5}, \frac{7}{15}$
সমাধানঃ
এখানে ভগ্নাংশগুলো হলো: $\frac{1}{3}, \frac{4}{5}$ এবং $\frac{7}{15}$
হরগুলির ল.সা.গু. করে পাই –
| 3 | 3, | 5, | 15 |
| 5 | 1, | 5, | 5 |
| 1, | 1, | 1 |
ল.সা.গু. = 3 × 5 × 1 × 1 × 1 = 15
$\frac{1}{3} = \frac{1 × 5}{3 × 5} = \frac{5}{15}$
$\frac{4}{5} = \frac{4 × 3}{5 × 3} = \frac{12}{15}$
$\frac{7}{15} = \frac{7 × 1}{15 × 1} = \frac{7}{15}$
∴ ছোট থেকে বড় হিসেবে সাজালে পাই = $\frac{1}{3}, \frac{7}{15}, \frac{4}{5}$ (উত্তর:)
(e) $\frac{5}{7}, \frac{3}{4}, \frac{1}{4}$
সমাধানঃ
এখানে ভগ্নাংশগুলো হলো: $\frac{5}{7}, \frac{3}{4}$ এবং $\frac{1}{4}$
হরগুলির ল.সা.গু. করে পাই –
| 4 | 7, | 4, | 4 |
| 7, | 1, | 1 |
ল.সা.গু. = 4 × 7 × 1 × 1 = 28
$\frac{5}{7} = \frac{5 × 4}{7 × 4} = \frac{20}{28}$
$\frac{3}{4} = \frac{3 × 7}{4 × 7} = \frac{21}{28}$
$\frac{1}{4} = \frac{1 × 7}{4 × 7} = \frac{7}{28}$
∴ ছোট থেকে বড় হিসেবে সাজালে পাই = $\frac{1}{4}, \frac{5}{7}, \frac{3}{4}$ (উত্তর:)
(f) $3\frac{1}{2}, 7\frac{5}{9}, 7\frac{1}{5}$
সমাধানঃ
এখানে ভগ্নাংশগুলো হলো: $3\frac{1}{2} = \frac{7}{2}$, $7\frac{5}{9} = \frac{68}{9}$ এবং $7\frac{1}{5} = \frac{36}{5}$
হরগুলির ল.সা.গু. করে পাই –
(যেহেতু সংখ্যাগুলোর মধ্যে কোনো সাধারণ উৎপাদক নেই)
∴ ল.সা.গু. = 2 × 9 × 5 = 90
$3\frac{1}{2}$ = $\frac{7}{2} = \frac{7 × 45}{2 × 45} = \frac{315}{90}$
$7\frac{5}{9}$ = $\frac{68}{9} = \frac{68 × 10}{9 × 10} = \frac{680}{90}$
$7\frac{1}{5}$ = $\frac{36}{5} = \frac{36 × 18}{5 × 18} = \frac{648}{90}$
∴ ছোট থেকে বড় হিসেবে সাজালে পাই = $\frac{7}{2}, \frac{36}{5}, \frac{68}{9}$ অর্থাৎ, $3\frac{1}{2}, 7\frac{1}{5}, 7\frac{5}{9}$ (উত্তর:)
(g) $\frac{1}{8}, \frac{7}{10}, \frac{3}{5}$
সমাধানঃ
এখানে ভগ্নাংশগুলো হলো: $\frac{1}{8}, \frac{7}{10}$ এবং $\frac{3}{5}$
হরগুলির ল.সা.গু. করে পাই –
| 2 | 8, | 10, | 5 |
| 5 | 4, | 5, | 5 |
| 4, | 1, | 1 |
ল.সা.গু. = 2 × 5 × 4 × 1 × 1 = 40
$\frac{1}{8} = \frac{1 × 5}{8 × 5} = \frac{5}{40}$
$\frac{7}{10} = \frac{7 × 4}{10 × 4} = \frac{28}{40}$
$\frac{3}{5} = \frac{3 × 8}{5 × 8} = \frac{24}{40}$
∴ ছোট থেকে বড় হিসেবে সাজালে পাই = $\frac{1}{8}, \frac{3}{5}, \frac{7}{10}$ (উত্তর:)
(h) $3\frac{1}{2}, 3\frac{5}{9}, 3\frac{1}{5}$
সমাধানঃ
এখানে ভগ্নাংশগুলো হলো: $3\frac{1}{2} = \frac{7}{2}$, $3\frac{5}{9} = \frac{32}{9}$ এবং $3\frac{1}{5} = \frac{16}{5}$
হরগুলির ল.সা.গু. করে পাই –
(যেহেতু সংখ্যাগুলোর মধ্যে কোনো সাধারণ উৎপাদক নেই)
∴ ল.সা.গু. = 2 × 9 × 5 = 90
$3\frac{1}{2}$ = $\frac{7}{2} = \frac{7 × 45}{2 × 45} = \frac{315}{90}$
$3\frac{5}{9}$ = $\frac{32}{9} = \frac{32 × 10}{9 × 10} = \frac{320}{90}$
$3\frac{1}{5}$ = $\frac{16}{5} = \frac{16 × 18}{5 × 18} = \frac{288}{90}$
∴ ছোট থেকে বড় হিসেবে সাজালে পাই = $\frac{16}{5}, \frac{7}{2}, \frac{32}{9}$ অর্থাৎ, $3\frac{1}{5}, 3\frac{1}{2}, 3\frac{5}{9}$ (উত্তর:)
8. মান বের করি –
(a) $\frac{2}{7} + \frac{2}{3} + 1\frac{1}{2}$
সমাধানঃ
$\frac{2}{7} + \frac{2}{3} + 1\frac{1}{2}$
$= \frac{2}{7} + \frac{2}{3} + \frac{3}{2}$
$= \frac{12 + 28 + 63}{42}$ [ ∵ 7, 3 ও 2 এর ল.সা.গু. = 42 ]
$= \frac{103}{42}$
$= 2\frac{19}{42}$
উত্তর: $2\frac{19}{42}$
(b) $1\frac{2}{5} – \frac{3}{8} + \frac{1}{4}$
সমাধানঃ
$1\frac{2}{5} – \frac{3}{8} + \frac{1}{4}$
$= \frac{7}{5} – \frac{3}{8} + \frac{1}{4}$
$= \frac{56 – 15 + 10}{40}$ [ ∵ 5, 8 ও 4 এর ল.সা.গু. = 40 ]
$= \frac{41 + 10}{40}$
$= \frac{51}{40}$
$= 1\frac{11}{40}$
উত্তর: $1\frac{11}{40}$
(c) $\frac{2}{5} + \frac{3}{8} – \frac{1}{4}$
সমাধানঃ
$\frac{2}{5} + \frac{3}{8} – \frac{1}{4}$
$= \frac{16 + 15 – 10}{40}$ [ ∵ 5, 8 ও 4 এর ল.সা.গু. = 40 ]
$= \frac{31 – 10}{40}$
$= \frac{21}{40}$
উত্তর: $\frac{21}{40}$
(d) $7 – 3\frac{1}{8} – 2\frac{1}{3}$
সমাধানঃ
$7 – 3\frac{1}{8} – 2\frac{1}{3}$
$= \frac{7}{1} – \frac{25}{8} – \frac{7}{3}$
$= \frac{168 – 75 – 56}{24}$ [ ∵ 1, 8 ও 3 এর ল.সা.গু. = 24 ]
$= \frac{93 – 56}{24}$
$= \frac{37}{24}$
$= 1\frac{13}{24}$
উত্তর: $1\frac{13}{24}$
(e) $\frac{4}{5} + \frac{5}{8} – 1\frac{1}{3}$
সমাধানঃ
$\frac{4}{5} + \frac{5}{8} – 1\frac{1}{3}$
$= \frac{4}{5} + \frac{5}{8} – \frac{4}{3}$
$= \frac{96 + 75 – 160}{120}$ [ ∵ 5, 8 ও 3 এর ল.সা.গু. = 120 ]
$= \frac{171 – 160}{120}$
$= \frac{11}{120}$
উত্তর: $\frac{11}{120}$
(f) $1\frac{3}{10} + 1\frac{4}{5} – 1\frac{1}{4}$
সমাধানঃ
$1\frac{3}{10} + 1\frac{4}{5} – 1\frac{1}{4}$
$= \frac{13}{10} + \frac{9}{5} – \frac{5}{4}$
$= \frac{26 + 36 – 25}{20}$ [ ∵ 10, 5 ও 4 এর ল.সা.গু. = 20 ]
$= \frac{62 – 25}{20}$
$= \frac{37}{20}$
$= 1\frac{17}{20}$
উত্তর: $1\frac{17}{20}$
(g) $2\frac{5}{6} – 1\frac{8}{9} + 1\frac{3}{4}$
সমাধানঃ
$2\frac{5}{6} – 1\frac{8}{9} + 1\frac{3}{4}$
$= \frac{17}{6} – \frac{17}{9} + \frac{7}{4}$
$= \frac{102 – 68 + 63}{36}$ [ ∵ 6, 9 ও 4 এর ল.সা.গু. = 36 ]
$= \frac{34 + 63}{36}$
$= \frac{97}{36}$
$= 2\frac{25}{36}$
উত্তর: $2\frac{25}{36}$
(h) $4\frac{1}{7} + 2\frac{2}{5} – 5$
সমাধানঃ
$4\frac{1}{7} + 2\frac{2}{5} – 5$
$= \frac{29}{7} + \frac{12}{5} – \frac{5}{1}$
$= \frac{145 + 84 – 175}{35}$ [ ∵ 7, 5 ও 1 এর ল.সা.গু. = 35 ]
$= \frac{229 – 175}{35}$
$= \frac{54}{35}$
$= 1\frac{19}{35}$
উত্তর: $1\frac{19}{35}$
9. হিসাব করি –
(a) $\frac{2}{3}$-এর সাথে কত যোগ করলে 2 পাব দেখি।
সমাধানঃ
$2 – \frac{2}{3}$
$= \frac{2}{1} – \frac{2}{3}$
$= \frac{6 – 2}{3}$
$= \frac{4}{3}$
উত্তর: $\frac{2}{3}$ এর সঙ্গে $\frac{4}{3}$ যোগ করলে 2 পাওয়া যাবে।
(b) আজ টিফিনের সময়ে স্কুলের সম্পূর্ণ ভরতি জলের ট্যাঙ্কের $\frac{1}{4}$ অংশ জল খরচ হয়েছে। ছুটির সময়ে দেখা গেল আরও $\frac{1}{3}$ অংশ জল খরচ হয়েছে। ছুটির পরে ট্যাঙ্কে কত অংশ জল পড়ে আছে দেখি।
সমাধানঃ
ধরি, সম্পূর্ণ জলের পরিমাণ = $1$ অংশ
টিফিনের সময় জল খরচ হয় = $\frac{1}{4}$ অংশ
এবং ছুটির সময় জল খরচ হয় = $\frac{1}{3}$ অংশ
∴ মোট জল খরচ হয় = $\frac{1}{4} + \frac{1}{3}$ অংশ
= $\frac{3 + 4}{12}$ অংশ
= $\frac{7}{12}$ অংশ
∴ জল বাকি থাকে = 1 – $\frac{7}{12}$ অংশ
= $\frac{12 – 7}{12}$ অংশ
= $\frac{5}{12}$ অংশ
উত্তর: ছুটির পরে ট্যাঙ্কে $\frac{5}{12}$ অংশ জল পড়ে আছে।
(c) আজ টিফিনে আমি কেক নিয়ে গিয়েছিলাম। আমার দুই বন্ধু আয়ূষ ও সাবানা আমার কেকের যথাক্রমে $\frac{1}{3}$ অংশ ও $\frac{2}{5}$ অংশ খেল। কেকের বাকি অংশটা আমি খেলাম। কে বেশি কেক খেল হিসাব করি।
সমাধানঃ
ধরি, সম্পূর্ণ কেকের পরিমাণ = 1 অংশ
আয়ুস খেয়েছে = $\frac{1}{3}$ অংশ
সাবানা খেয়েছে = $\frac{2}{5}$ অংশ
∴ আয়ুস ও সাবানা দুজনে মিলে মোট খেয়েছে =
$\frac{1}{3} + \frac{2}{5}$ অংশ
= $\frac{5 + 6}{15}$ অংশ
= $\frac{11}{15}$ অংশ
∴ কেক বাকি আছে =
= 1 – $\frac{11}{15}$ অংশ
= $\frac{15 – 11}{15}$ অংশ
= $\frac{4}{15}$ অংশ
∴ আমি খেলাম কেকের $\frac{4}{15}$ অংশ।
আয়ুস খায়: $\frac{1}{3}$ অংশ = $\frac{1 \times 5}{3 \times 5} = \frac{5}{15}$ অংশ।
সাবানা খায়: $\frac{2}{5}$ অংশ = $\frac{2 \times 3}{5 \times 3} = \frac{6}{15}$ অংশ।
আমি খাই: $\frac{4}{15}$ অংশ = $\frac{4 \times 1}{15 \times 1} = \frac{4}{15}$ অংশ।
∵ $\frac{6}{15}$ > $\frac{5}{15}$ > $\frac{4}{15}$
∴ সাবানা সবথেকে বেশি কেক খেয়েছে। (উত্তর:)
(d) রতনবাবু তাঁর 25 বিঘা জমির মধ্যে 16 বিঘা জমিতে পাট চাষ করেছেন। কিন্তু উমাদেবী তাঁর 15 বিঘা জমির মধ্যে 8 বিঘা জমিতে পাট চাষ করেছেন। হিসাব করে দেখি রতনবাবু ও উমাদেবী তাঁদের জমির কত অংশে পাট চাষ করেছেন ও কে বেশি পরিমাণ জমিতে পাট চাষ করেছেন।
সমাধানঃ
রতনবাবুর মোট জমির পরিমাণ = 25 বিঘা।
এবং তিনি পাট চাষ করেন = 16 বিঘাতে।
∴ রতনবাবু পাট চাষ করেন = $\frac{16}{25}$ অংশ জমিতে।
উষাদেবীর মোট জমির পরিমাণ = 15 বিঘা।
এবং তিনি পাট চাষ করেন = 8 বিঘাতে।
∴ উষাদেবী পাট চাষ করেন = $\frac{8}{15}$ অংশ জমিতে।
রতনবাবু পাট চাষ করেন = $\frac{16}{25}$ অংশ = $\frac{16 \times 3}{25 \times 3}$ = $\frac{48}{75}$
তপনবাবু পাট চাষ করেন = $\frac{8}{15}$ অংশ = $\frac{8 \times 5}{15 \times 5}$ = $\frac{40}{75}$
∴ $\frac{48}{75} > \frac{40}{75}$
∴ রতনবাবু বেশি জমিতে পাট চাষ করেছেন। (উত্তর:)
(e) আমার 15 মিটার লম্বা সাদা ফিতে আছে। আমি $\frac{1}{3}$ অংশ কেটে নিলাম। কত অংশ সাদা ফিতে পড়ে রইল ও সেটি কতটা লম্বা বের করি।
সমাধানঃ
আমার মোট ফিতের পরিমাণ = 15 মিটার।
∴ ফিতে কেটে নিয়েছি = 15 মিটারের $\frac{1}{3}$ অংশ।
= $\overset5{\cancel{15}}$ × $\frac{1}{\cancel3}$ = 5 মিটার।
∴ ফিতে পড়ে থাকে = (15 – 5) মিটার = 10 মিটার।
বা, $\frac{\overset2{\cancel{10}}}{\overset3{\cancel{15}}}$ অংশ = $\frac{2}{3}$ অংশ।
∴ ফিতে পড়ে থাকে $\frac{2}{3}$ অংশ বা 10 মিটার।
∴ $\frac{2}{3}$ অংশ সাদা ফিতে পড়ে রইল ও সেটি 10 মিটার লম্বা। (উত্তর:)
আরো পড়ুন
Class 6 Math Koshe Dekhi 1.1 Solution | কষে দেখি 1.1 সরল অঙ্ক সমাধান
Class 6 Math Koshe Dekhi 1.2 Solution | কষে দেখি 1.2 গসাগু ও লসাগু সমাধান
Note: এই আর্টিকেলের ব্যাপারে তোমার মতামত জানাতে নীচে দেওয়া কমেন্ট বক্সে গিয়ে কমেন্ট করতে পারো। ধন্যবাদ।
