এই আর্টিকেলে আমরা মাধ্যমিক গণিত সমাধান Theorems related to Angles Koshe Dekhi 7.1 নিয়ে এসেছি। Class 10 Theorems related to Angles Koshe Dekhi 7.1 Answer solve | Class X Theorems related to Angles Koshe Dekhi 7.1 | মাধ্যমিক গণিতের সপ্তম অধ্যায় বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.১ থেকে সমস্ত প্রশ্ন ও উত্তর নিয়ে এখানে আলোচনা করা হয়েছে। মাধ্যমিক গণিত প্রকাশ বইয়ের সমস্ত অধ্যায়ের উত্তর পেতে এই লিঙ্কে ক্লিক করো।
বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য
Theorems related to Angles in a Circle
কষে দেখি ৭.১
Class 10 Theorems related to Angles Koshe Dekhi 7.1 Solution
1. ABC সমদ্বিবাহু ত্রিভুজের AB=AC. সমদ্বিবাহু ত্রিভুজটির পরিকেন্দ্র O এবং BC বাহুর যেদিকে A বিন্দু অবস্থিত তার বিপরীত পার্শ্বে কেন্দ্র O অবস্থিত । ∠BOC= 100° হলে ∠ ABC ও ∠ ABO এর মান হিসাব করে লিখি ।
সমাধানঃ

∆ABC সমদ্বিবাহু ত্রিভুজের AB=AC.বৃত্তের কেন্দ্র O , BC বাহুর বিপরীত পার্শ্বে অবস্থিত ।∠ABC ও ∠ ABO এর মাণ নির্ণয় করতে হবে ।
BOC = 100° ( প্রদত্ত)
এখন BAC বৃত্ত চাপের ওপর প্রবিদ্ধ কোণ∠BOC হল কেন্দ্রস্থ কোণ এবং কোণ ∠BAC হল পরিধিস্থ কোণ
∴∠ BOC=2∠BAC
সুতরাং , ∠BAC = `\frac{1}{2}` প্রবিদ্ধ কোণ ∠BOC
= `\frac{1}{2}` (360°-100°)
=`\frac{1}{2}` ✕ 260°
=130°
এখন , ত্রিভুজ ∆BAC এর ক্ষেত্রে ,
AB=AC
∴ ∠ABC = ∠ACB
আবার কোণ ∠BAC = 130°
সুতরাং , ∠ABC = ∠ACB = `\frac{(180°-∠BAC)}{2} = \frac{(180°-130°)}{2}` = 25°
ত্রিভুজ ∆OBC এর ক্ষেত্রে OB=OC
সুতরাং , ∠OBC = ∠OCB
আবার , কোণ ∠BOC = 100°
∴ ∠OBC =∠ OCB = `\frac{(180°-100°)}{2}`= 40°
সুতরাং ∠ABO = ∠ABC+∠OBC = 25°+40° =65°
∴ ∠ABC = 25° এবং ∠ABO = 65° (উত্তর)
2. পাশের চিত্রে ত্রিভুজ ABC এর পরিবৃত্তের কেন্দ্র O এবং ∠ AOC = 110° ; ∠ABC এর মাণ হিসাব করে লিখি ।
সমাধানঃ
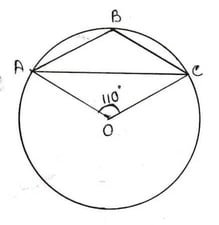
ABC বৃত্ত চাপের ওপর প্রবিদ্ধ কোণ ∠AOC কেন্দ্রস্থ কোণ এবং ∠ABC পরিধিস্থ কোণ
সুতরাং , ∠ABC = `\frac{1}{2}` প্রবিদ্ধ কোণ ∠AOC
∴ ∠ABC = `\frac{1}{2}`(360°-110°)= `\frac{1}{2}`✕250° = 125°
3.O কেন্দ্রীয় বৃত্তের ABCD হল একটি বৃত্তস্থ চতুর্ভুজ । DC বাহুকে P পর্যন্ত বর্ধিত করা হল । ∠BCP = 108 হলে ∠BOD এর মাণ হিসাব করে লিখি ।
সমাধানঃ
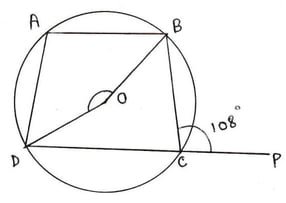
O কেন্দ্রীয় বৃত্তের ABCD হল একটি বৃত্তস্থ চতুর্ভুজ । DC বাহুকে P পর্যন্ত বর্ধিত করা হল
∠BCP = 108°
∴∠ BCD = 180°-108°=72°
এখন , BCD বৃত্ত চাপের ওপর কোণ ∠BOD কেন্দ্রস্থ কোণ এবং কোণ ∠BCD পরিধিস্থ কোণ
∴ ∠BOD = 2∠BCD = 2✕72°=144°
4. পাশের চিত্রে O কেন্দ্রীয় বৃত্তের ∠AOD =40° এবং ∠ACB = 35° ; ∠ BCO এবং ∠ BOD এর মাণ হিসাব করে লিখি ও উত্তরের সপক্ষে যুক্তি দিই ।
সমাধানঃ
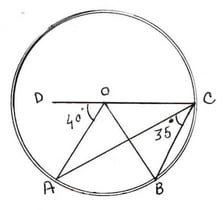
∠AOD = 40° এবং ∠ACB = 35°
বৃত্তটির কেন্দ্রস্থ কোণ ∠DOA এবং পরিধিস্থ কোণ ∠DCA
∴ ∠DOA = 2 ∠DCA
Or, ∠DCA = `\frac{1}{2}`∠DOA = `\frac{1}{2}`✕40° = 20°
∴ ∠BCO = ∠DCA+∠ACB= 20°+35° = 55°
আবার ,AB বৃত্ত চাপের ওপর AOB কেন্দ্রস্থ কোণ এবং ACB পরিধিস্থ কোণ
সুতরাং , ∠AOB = 2∠ACB = 2✕ 35° = 70°
∴ ∠BOD = ∠AOB+∠AOD = 70°+40°=110°
∴∠ BCO = 55° এবং ∠BOD = 110° ( উত্তর)
5. পাশের চিত্রে O কেন্দ্রীয় বৃত্তের ∠ APB = 80° হলে ∠AOB ও ∠COD এর মানের সমষ্টি নির্ণয় করি ও উভয় উত্তরের সপক্ষে যুক্তি দিই ।
সমাধানঃ
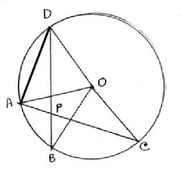
O কেন্দ্রীয় বৃত্তের ∠APB = 80°
∠AOB ও ∠COD এর মানের সমষ্টি নির্ণয় করতে হবে
A,D যুক্ত করা হল ।
AB বৃত্ত চাপের ওপর ∠AOB কেন্দ্রস্থ কোণ এবং ∠ADB পরিধিস্থ কোণ
∴ ∠AOB =2 ∠ADB—–(i)
আবার , CD বৃত্ত চাপের ওপর ∠COD কেন্দ্রস্থ কোণ এবং ∠CAD পরিধিস্থ কোণ
∴ ∠COD = 2∠CAD—–(ii)
এখন ∆APD ত্রিভুজে বহিঃস্থ কোণ ∠APB = ∠PAD+∠ADP [∵কোনো ত্রিভুজের একটি বহিঃস্থ কোণ,অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]
∴ ∠APB=∠PAD+∠ADP
বা, ∠APB=∠CAD+∠ADB [∵∠PAD =∠CAD এবং ∠ADP = ∠ADB ]
বা, ∠CAD+∠ADB = 80° [∵∠APB = 80°] —-(iii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই ,
∠AOB+∠COD
=2∠ADB+2∠CAD
=2(∠ADB+∠CAD)
=2✕ 80° [ (iii) নং সমীকরণ থেকে পাই ]
= 160°
6.পাশের ছবির মত C ও D কেন্দ্র বিশিষ্ট দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা PQ অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে । প্রমান করি যে ,
(i) ∠ PBQ = ∠CAD
(ii) ∠BPC = ∠BQD
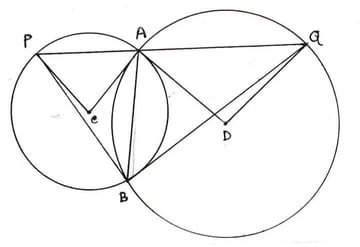
C ও D কেন্দ্র বিশিষ্ট দুটি বৃত্ত, যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা PQ অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে । প্রমান করতে হবে যে ,
(i) ∠ PBQ = ∠ CAD
(ii) ∠ BPC = ∠ BQD
(i)
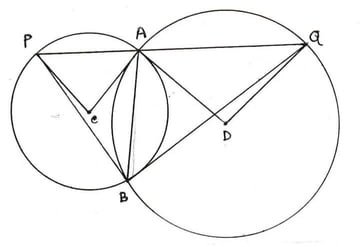
প্রমানঃ AP বৃত্ত চাপের ওপর ∠ACP কেন্দ্রস্থ কোণ এবং ∠ABP পরিধিস্থ কোণ
সুতরাং , ∠ABP = `\frac{1}{2}`∠ACP —– (1)
আবার , AQ বৃত্ত চাপের ওপর ∠ ADQ কেন্দ্রস্থ কোণ এবং ∠ ABQ পরিধিস্থ কোণ
∴ ∠ABQ = `\frac{1}{2}`∠ADQ —–(2)
এখন , ত্রিভুজ ∆ACP এর ক্ষেত্রে CA=CP [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠CAP= ∠CPA
∴ ∠ACP = (180º-2∠CAP) —-(3)
ত্রিভুজ ∆ADQ এর ক্ষেত্রে AD=DQ [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠DAQ = ∠DQA
∴ ∠ADQ = ( 180º -2∠DAQ) —–(4)
এখন , (1) নং ও (2) নং সমীকরণ যোগ করে পাই ,
∠ABP+∠ABQ
= `\frac{1}{2}`∠ACP+`\frac{1}{2}`∠ADQ
= `\frac{1}{2}`(∠ACP+∠ADQ)
= `\frac{1}{2}`{( 180º-2∠CAP)+(180º-2∠DAQ)} [(3) ও (4) নং সমীকরণ থেকে পাই ]
= `\frac{1}{2}`{360º -2(∠CAP+∠DAQ)}
=`\frac{1}{2}` {360º -2(180-∠CAD)}[∵∠PAQ=1 সরলকোণ ]
=`\frac{1}{2}` (360º -360º +2∠CAD)
= ∠CAD
∴ ∠ABP+ABQ =∠CAD
বা, ∠PBQ = ∠CAD [ প্রমাণিত ]
(ii)

অঙ্কনঃ C,B ; B,D যুক্ত করা হল ।
প্রমানঃ ACBD চতুর্ভুজের ক্ষেত্রে , BC =AC [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠CBA = ∠CAB —-(1)
আবার , BD = DA [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠DBA = ∠DAB —-(2)
(i) ও (ii) নং সমীকরণ যোগ করে পাই ,
∠CBA+∠DBA = ∠CAB+∠DAB
বা, ∠CBD=∠CAD —-(3)
আবার , ∠PBQ = ∠CAD [ পূর্বে প্রমাণিত ]
∴ ∠CBD = ∠PBQ
বা, ∠CBQ+∠DBQ = ∠CBP+∠CBQ
বা, ∠DBQ = ∠CBP—-( 4)
আবার , ∠DBQ = ∠DQB [∵ DB =DQ , একই বৃত্তের ব্যাসার্ধ ]—(5)
এবং , ∠CBP = ∠CPB [∵CB = CP , একই বৃত্তের ব্যাসার্ধ ]—(6)
∴ ∠DQB = ∠CPB [ 4,5 এবং 6 থেকে পাই ]
বা, ∠BPC = ∠BQD [ প্রমাণিত ]
7. ABC ত্রিভুজের পরিকেন্দ্র O ; প্রমান করি যে , ∠OBC+∠BAC = 90°
প্রমানঃ
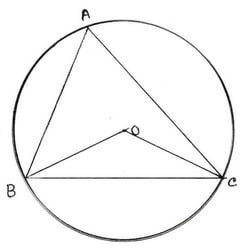
∆ABC ত্রিভুজের পরিকেন্দ্র O ।
এখন , BC বৃত্ত চাপের ওপর ∠BOC কেন্দ্রস্থ কোণ এবং ∠BAC পরিধিস্থ কোণ
∴ ∠BAC = `\frac{1}{2}`∠BOC —-(1)
আবার , ত্রিভুজ ∆BOC এর ক্ষেত্রে ,
OB = OC [একই বৃত্তের ব্যসার্ধ ]
∴ ∠OBC =∠OCB
∴ ∠OBC = `\frac{( 180°–∠BOC)}{2}`- —(2)
এখন , ∠OBC+∠BAC
= `\frac{(180°-∠BOC)}{2} +\frac{1}{2}`∠BOC
= 90°- `\frac{1}{2}`∠BOC + `\frac{1}{2}`∠BOC
=90°
∴ ∠OBC+∠BAC =90°[ প্রমাণিত ]
8. দুটি সমান বৃত্ত একটি অপরটির কেন্দ্রগামী এবং বৃত্তদুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করলে , প্রমান করি যে ত্রিভুজ ∆BCD সমবাহু ত্রিভুজ ।

মনে করি, বৃত্ত দুটির কেন্দ্র যথাক্রমে P এবং Q
অঙ্কনঃ PA ,PB ,BQ,QA এবং PQ অঙ্কন করা হল ।
প্রমানঃ ∆APQ এর AP=PQ=AQ [ যেহেতু বৃত্ত দুটি সমান সুতরাং তাদের ব্যাসার্ধ সমান ]
∴ ∆APQসমবাহু ত্রিভুজ
∴ ∠APQ=∠AQP=60∘
অনুরূপে , ∆BPQ সমবাহু ত্রিভুজ ।
∴ ∠BPQ = ∠BQP = 60∘
এখন , ∠APB=∠APQ+∠BPQ
∴ ∠APB = 60°+60°
∴ ∠APB = 120°
অনুরূপে , ∠AQB = 120°
এখানে, AQB বৃত্তচাপের ওপর ∠APB কেন্দ্রস্থ কোণ এবং ∠ACB পরিধিস্থ কোণ
সুতরাং , ∠ACB = `\frac{1}{2}`✕ ∠APB = `\frac{1}{2}`✕ 120° = 60°
এবং , APB বৃত্তচাপের ওপর ∠AQB কেন্দ্রস্থ কোণ এবং ∠ADB পরিধিস্থ কোণ
∴ ∠ADB = `\frac{1}{2}`∠AQB = `\frac{1}{2}`✕120° = 60°
∴ ∆BCD ত্রিভুজে ∠BDC = ∠BCD = ∠CBD = 60°
∴ ∆BCD সমবাহু ত্রিভুজ (প্রমাণিত)
9. ABC ত্রিভুজের পরিবৃত্তের কেন্দ্র S এবং AD⊥BC হলে , প্রমান করি যে ∠BAD = ∠SAC
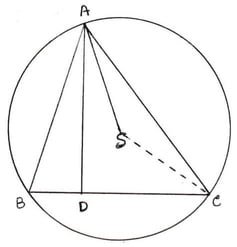
∆ABC ত্রিভুজের পরিবৃত্তের কেন্দ্র S এবং AD ⊥ BC । প্রমান করতে হবে ∠BAD = ∠SAC
অঙ্কনঃ S,C যুক্ত করা হল ।
প্রমানঃ ত্রিভুজ ∆ASC এর ক্ষেত্রে ,
AS =SC
∴ ∠SAC = ∠SCA
∴ ∠SAC= `\frac{(180°-∠ASC)}{2}` = 90 – `\frac{1}{2}`☓ ∠ ASC —-(i)
আবার , ∠ABC = `\frac{1}{2}`✕∠ASC [ যেহেতু একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন ]—-(ii)
∴ ∠SAC = 90-∠ABC [(i) ও (ii) থেকে পাই ]
আবার , ∠ABD+∠BAD = 90∘ [যেহেতু ∠ADB = 90∘ কারণ AD⊥BC ]
∴∠BAD = 90∘ – ∠ABD
⇒∠BAD = 90∘ – ∠ABC
∴ ∠SAC = ∠BAD
∴ ∠BAD = ∠SAC [ প্রমাণিত ]
10. O কেন্দ্রীয় বৃত্তের দুটি জ্যা AB ও CD পরস্পরকে P বিন্দুতে ছেদ করেছে । প্রমান করি যে ∠AOD +∠BOC = 2∠BPC
যদি ∠AOD ও ∠BOC পরস্পর সম্পূরক হয় তাহলে প্রমান করি যে , জ্যা দুটি পরস্পর লম্ব ।
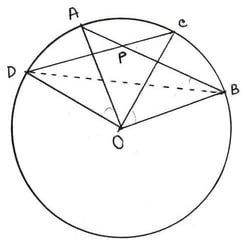
O কেন্দ্রীয় বৃত্তের দুটি জ্যা AB ও CD পরস্পরকে P বিন্দুতে ছেদ করেছে
প্রমান করতে হবে যে, ∠AOD +∠BOC = 2∠BPC
অঙ্কনঃ B,D যুক্ত করা হল ।
প্রমানঃ AD বৃত্তচাপের ওপর ∠AOD কেন্দ্রস্থ কোণ এবং ∠ABD পরিধিস্থ কোণ
∴ ∠AOD = 2∠ABD ———-(i)
আবার , BC বৃত্তচাপের ওপর ∠BOC কেন্দ্রস্থ কোণ এবং ∠BDC পরিধিস্থ কোণ
∴ ∠BOC = 2∠BDC ——(ii)
আবার ত্রিভুজ ∆PDB এর ক্ষেত্রে ,
∠PBD+∠PDB
= ∠ABD+ ∠BDC
= ∠BPC [ যেহেতু ত্রিভুজের বহিঃস্থ কোণ , অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]—(iii)
এখন (i) ও (ii) যোগ করে পাই ,
∠AOD+∠BOC = 2(∠ABD+∠BDC) = 2∠BPC [ (iii) থেকে পাই ]
∴ ∠AOD+∠BOC = 2∠BPC [ প্রমাণিত ]
আবার , ∠AOD এবং ∠BOC পরস্পর সম্পূরক হলে ,
∠AOD+∠BOC=180°
বা, 2∠BPC = 180° [∵ ∠AOD+∠BOC = 2∠BPC, পূর্বে প্রমাণিত ]
বা, ∠BPC = 90°
সুতরাং AB ও CD জ্যা দুটি পরস্পর লম্ব ।
11. O কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জ্যা কে বর্ধিত করলে তারা পরস্পরকে P বিন্দুতে ছেদ করলে , প্রমান করি যে , ∠AOC –∠BOD = 2∠BPC

O কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জ্যা কে বর্ধিত করলে তারা পরস্পরকে P বিন্দুতে ছেদ করে । প্রমাণ করতে হবে যে, ∠AOC –∠BOD = 2∠BPC
অঙ্কনঃ A,D যুক্ত করা হল ।
প্রমানঃ AC বৃত্তচাপের ওপর ∠AOC কেন্দ্রস্থ কোণ এবং ∠ADC পরিধিস্থ কোণ
∴ ∠AOC = 2∠ADC —-(i)
আবার , BD বৃত্তচাপের ওপর ∠BOD কেন্দ্রস্থ কোণ এবং ∠BAD পরিধিস্থ কোণ
∴ ∠BOD = 2 ∠BAD —-(ii)
আবার ত্রিভুজ ∆APD এর ক্ষেত্রে ,
∠ADC = ∠APD +∠PAD [∵ত্রিভুজের বহিঃস্থ কোণ , অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]
∴ ∠ADC-∠PAD = ∠APD —–(iii)
(i) থেকে (ii) বিয়োগ করে পাই ,
∠AOC – ∠BOD
= 2(∠ADC-∠BAD)
=2 (∠ADC-∠PAD) [∵∠BAD = ∠PAD]
= 2∠APD
= 2∠BPC [∵ ∠APD = ∠BPC]
∴ ∠AOC-∠BOD =2∠BPC [প্রমাণিত]
12.ABCD চতুর্ভুজের A বিন্দুকে কেন্দ্র করে একটি বৃত্ত অঙ্কন করা হল যেটি B , C ও D বিন্দু দিয়ে যায় । প্রমান করি যে CBD+CDB = `\frac{1}{2}`BAD ।
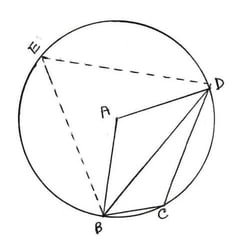
ABCD চতুর্ভুজের A বিন্দুকে কেন্দ্র করে একটি বৃত্ত অঙ্কন করা হল যেটি B , C ও D বিন্দু দিয়ে যায় । প্রমাণ করতে হবে ∠CBD+∠CDB =`\frac{1}{2}`∠BAD
অঙ্কনঃ বৃত্তের পরিধির ওপর E একটি বিন্দু , BE এবং DE অঙ্কন করা হল ।
প্রমানঃ ত্রিভুজ ∆BCD এর ক্ষেত্রে ,
∠CBD+∠CDB
= 180° –∠BCD [ যেহেতু ত্রিভুজের তিনটি কোণের সমষ্টি 180°]
= ∠BED [ যেহেতু বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি সম্পূরক ∴ ∠BCD+∠BED=180° ]
= `\frac{1}{2}`∠BAD [ BED বৃত্তচাপের ওপর ∠BAD কেন্দ্রস্থ কোণ এবং ∠BED পরিধিস্থ কোণ । এবং একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন ]
∴ ∠CBD+∠CDB = `\frac{1}{2}`∠BAD [প্রমাণিত]
13.ABC এর পরিকেন্দ্র O এবং OD ,BC বাহুর উপর লম্ব । প্রমাণ করি যে ∠BOD = ∠BAC ।
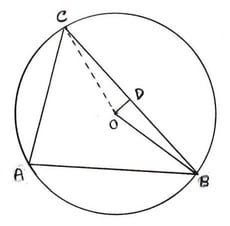
ABC এর পরিকেন্দ্র O এবং OD ,BC বাহুর উপর লম্ব ।
প্রমাণ করতে হবে , ∠BOD = ∠BAC
অঙ্কনঃ OC অঙ্কন করা হল ।
প্রমাণ: ∆BOD ও ∆COD এর ক্ষেত্রে,
∠ODB = ∠ODC =90∘ [ যেহেতু OD⊥ BC ]
OB = OC [ একই বৃত্তের ব্যাসার্ধ ]
OD সাধারণ বাহু
∴ ∆BOD ≅ ∆COD
∴ ∠BOD = ∠COD
∴ ∠BOD =`\frac{1}{2}`✕∠BOC = `\frac{1}{2}`✕2✕∠BAC = ∠BAC
∴∠BOD = ∠BAC [ প্রমাণিত ]
14. অতি সংক্ষিপ্ত প্রশ্ন (M.C.Q):
(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q):
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং PQ ব্যাস হলে , x এর মাণ কত ?
(a) 140°
(b) 40°
(c) 80°
(d) 20°
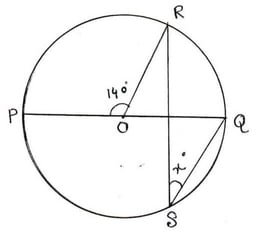
Ans: (d) 20°
সমাধানঃ ∠POR = 140°
∴ ∠ROQ = 180°-140° =40°
এখন , RQ বৃত্তচাপের উপর ∠ROQ কেন্দ্রস্থ কোণ এবং ∠RSQ পরিধিস্থ কোণ
∴ ∠RSQ=`\frac{1}{2}` ✕∠ROQ=`\frac{1}{2}`✕40°=20°
সুতরাং , x = 20°
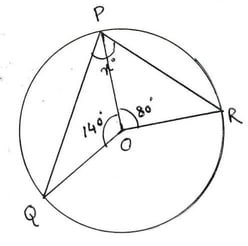
(ii) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে , x এর মাণ
(a) 70°
(b) 60°
(c ) 40°
(d) 20°
Ans: (a) 70°
সমাধানঃ
∠POQ =140° এবং ∠POR = 80°
∴ ∠QOR = 360°-(140°+80°) = 360°-220° = 140°
এখন , QR বৃত্তচাপের উপর ∠QOR কেন্দ্রস্থ কোণ এবং ∠QPR পরিধিস্থ কোণ
∠QPR = `\frac{1}{2}`✕∠QOR = `\frac{1}{2}`✕140° = 70°
∴ x = 70°
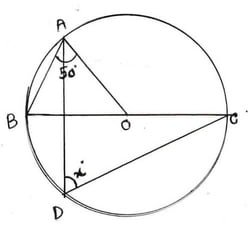
(iii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং BC ব্যাস হলে ,x এর মাণ
(a) 60°
(b) 50°
(c) 100°
(d) 80°
Ans: (b) 50°
সমাধানঃ OA =OB [একই বৃত্তের ব্যাসার্ধ ]
∴ ∠OAB = ∠OBA =50°
∴ ∠AOC = ∠OAB+∠OBA =50°+50° =100° [∵ কোনো ত্রিভুজের বহিঃস্থ কোণের মাণ অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]
আবার AC বৃত্তচাপের উপর ∠AOC কেন্দ্রস্থ কোণ এবং ∠ADC পরিধিস্থ কোণ
∴ ∠AOC = 2∠ADC
বা, ∠ADC = `\frac{1}{2}` ✕∠AOC
বা, ∠ADC = `\frac{1}{2}`✕100°
বা, ∠ADC = 50°
(iv) BC ত্রিভুজের O পরিকেন্দ্র । ∠OAB =50° হলে ∠ACB এর মাণ
(a) 50°
(b)100°
(c)40°
(d)80°

Ans: (c ) 40°
সমাধানঃ ∠OAB = 50°
∠OBA=50° [ OA=OB , একই বৃত্তের ব্যাসার্ধ ]
∴ ∠AOB = 180°-(∠OAB+∠OBA) =180°-(50°+50°) =80°
আবার , AB বৃত্তচাপের ওপর ∠AOB কেন্দ্রস্থ কোণ এবং ∠ACB পরিধিস্থ কোণ
∠ACB=`\frac{1}{2}`✕∠AOB [∵একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন ]
বা,∠ACB=`\frac{1}{2}`✕ 80°
বা, ∠ACB=40°
(v) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে , PQR এর মাণ
(a) 20°
(b) 40°
(c ) 60°
(d) 80°

Ans: (c ) 60°
ত্রিভুজ ∆OPQ তে , OP =OQ
∴ ∠OPQ =∠OQP =10°
∴ ∠POQ = 180°-(10°+10°) = 160°
আবার ,∆ORQ ত্রিভুজে OQ =OR [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠ORQ =∠OQR =40°
∴ ∠ROQ = 180°-(40°+40°) = 100°
এখন , ∠POR = ∠POQ – ∠ROQ = 160°-100° = 60°
(B) সত্য বা মিথ্যা লিখিঃ
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে , ∠AOB = 2∠ACD
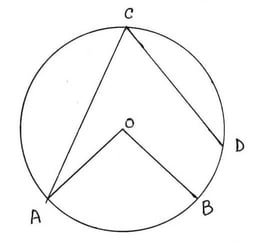
উত্তরঃ মিথ্যা
কারণ AB এবং AD দুটি ভিন্ন বৃত্তচাপ ।
(ii) ABC ত্রিভুজের ক্ষেত্রের ভিতর O বিন্দু এমনভাবে অবস্থিত যে OA=OB এবং ∠AOB = 2∠ACB । O বিন্দুকে কেন্দ্র করে OA দৈর্ঘ্য এর ব্যাসার্ধ নিয়ে বৃত্ত অঙ্কন করলে C বিন্দু বৃত্তের ওপর অবস্থিত হবে ।
উত্তরঃ সত্য ।
কারণ ∠AOB = 2 ∠ACB সুতরাং একই বৃত্তচাপ AB এর ওপর অবস্থিত ∠AOB কেন্দ্রস্থ কোণ এবং ∠ACB পরিধিস্থ কোণ । সুতরাং C বিন্দু বৃত্তের ওপর অবস্থিত হবে ।
(C ) শূন্যস্থান পূরণ করিঃ
(i) একই চাপের উপর অবস্থিত বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের ___________ ।
উত্তরঃ অর্ধেক
(ii) O কেন্দ্রীয় বৃত্তে AB ও AC জ্যা দুটির দৈর্ঘ্য সমান । ∠APB ও ∠DQC বৃত্তস্থ কোণ হলে কোণ দুটির মান __________ ।
উত্তরঃ সমান
(iii) একটি সমবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O হলে , যে কোনো একটি বাহু দ্বারা উৎপন্ন সম্মুখ কেন্দ্রস্থ কোণের মান _______________ ।
উত্তরঃ 120°
15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A)
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র । ∠OAB = 40° , ∠ABC=120° , ∠BCO = y এবং ∠COA = x হলে x ও y এর মাণ নির্ণয় করো ।
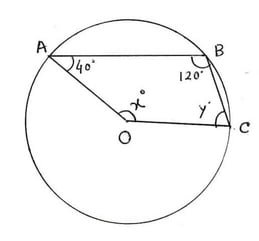
সমাধানঃ AC বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ ,প্রবিদ্ধ ∠AOC এবং পরিধিস্থ কোণ ∠ABC ।
∴ ∠ABC = `\frac{1}{2}`প্রবিদ্ধ ∠AOC [∵একই বৃত্তচাপের ওপর অবস্থিত পরিধিস্থ কোণ কেন্দ্রস্থ কোণের অর্ধেক ]
∴ 120° = `\frac{1}{2}`(360°-x)
⇒ 240°=360°-x
⇒ x=360°-240°
⇒ x=120°
∴ y=360°-(40°+120°+120°) = 360°-280°=80° [∵ চতুর্ভুজের চারটি কোণের সমষ্টি 360°]
∴x=120°, y=80° [উত্তর]
(ii) ABC ত্রিভুজের পরিকেন্দ্র O এবং D , BC এর মধ্যবিন্দু । ∠BAC = 40° হলে , ∠BOD এর মাণ নির্ণয় করো ।
সমাধানঃ
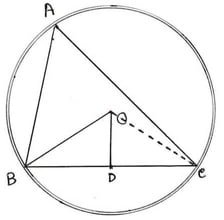
অঙ্কনঃ OC অঙ্কন করা হল ।
প্রমানঃ BAC বৃত্তচাপের ওপর ∠BAC পরিধিস্থ কোণ এবং ∠BOC কেন্দ্রস্থ কোণ ।
∠BOC =2∠BAC=2 ✕40° =80°
∆BOD ও ∆ COD এর ক্ষেত্রে ,
BD=DC [∵ D,BC এর মধ্যবিন্দু ]
OB = OC [ একই বৃত্তের ব্যাসার্ধ ]
OD সাধারণ বাহু
∴ BOD ≅ COD [বাহু-বাহু-বাহু শর্তানুসারে ]
∴ ∠BOD = ∠COD
আবার ∠BOC = 80°
∴ ∠BOD = ∠COD =40°
∴ ∠BOD=40° [উত্তর]
(iii) O কেন্দ্রীয় বৃত্তের উপর A ,B ,C তিনটি বিন্দু এমন ভাবে অবস্থিত যে AOCB একটি সামান্তরিক । ∠AOC এর মাণ নির্ণয় করি ।
সমাধানঃ

AOCB একটি সমান্তরিক ।
∴∠AOC = ∠ABC [∵ সামান্তরিকের বিপরীত কোণগুলি পরস্পর সমান ]—(i)
আবার , ∠ABC = `\frac{1}{2}`প্রবিদ্ধ ∠AOC [∵একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন ]—(ii)
(i) ও (ii) থেকে পাই ,
∴∠AOC=`\frac{1}{2}`প্রবিদ্ধ ∠AOC—(iii)
আবার, ∠AOC+প্রবিদ্ধ ∠AOC=360°
বা, `\frac{1}{2}`প্রবিদ্ধ ∠AOC+প্রবিদ্ধ ∠AOC=360° [(iii) থেকে পাই ]
বা, `\frac{3}{2}` ✕ (প্রবৃদ্ধ ∠AOC) = 360°
বা, 360°–∠AOC = 360° ✕ `\frac{2}{3}`
বা, ∠AOC =360°– 240°
বা, ∠AOC =120°
(iv) ABC সমদ্বিবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O এবং ∠ABC = 120° ; বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. হলে , AB বাহুর দৈর্ঘ্য নির্ণয় করি ।
সমাধানঃ
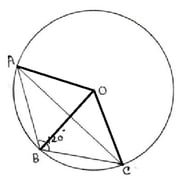
O,A;O,B;O,C যুক্ত করা হল ।
∆OAB এবং ∆OCB এর মধ্যে,
OA=OC [একই বৃত্তের ব্যাসার্ধ ]
OB সাধারণ বাহু
AB=BC [ ∆ABC সমদ্বিবাহু ত্রিভুজ ]
∴∆OAB ≅ ∆OCB [বাহু-বাহু-বাহু শর্তানুসারে]
∴ ∠OBA=∠OBC=60° [∵∠ABC =120° ]
আবার, ∠OAB=∠OBA=60° [∵OA=OB একই বৃত্তের ব্যাসার্ধ]
∴ ∠AOB=60° [∵ ত্রিভুজের তিনটি কোণের সমষ্টি 180° ]
∴ ত্রিভুজ AOB -এর ∠OAB=∠OBA=∠AOB=60°
∴ AOB সমবাহু ত্রিভুজ ।
∴ OA=OB=AB =5 সেমি.
∴ AB=5 সেমি.[উত্তর]
(V) A ও B কেন্দ্রীয় বৃত্তদ্বয় C ও D বিন্দুতে ছেদ করে । A কেন্দ্রীয় বৃত্তের উপর অপর বৃত্তের কেন্দ্র B অবস্থিত । ∠CQD =70° হলে ∠CPD এর মান নির্ণয় করি ।
সমাধানঃ

B,C ; B,D যুক্ত করা হল ।
CD বৃত্তচাপের ওপর ∠CBD কেন্দ্রস্থ কোণ এবং ∠CQD পরিধিস্থ কোণ
∴ ∠CBD =2✕∠CQD =2✕70°=140°
আবার, ∠CBD+∠CPD=180° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
⇒ ∠CPD= 180°–∠CBD
⇒ ∠CPD=180°-140°
⇒ ∠CPD=40° [উত্তর]
1. ABC সমদ্বিবাহু ত্রিভুজের AB=AC. সমদ্বিবাহু ত্রিভুজটির পরিকেন্দ্র O এবং BC বাহুর যেদিকে A বিন্দু অবস্থিত তার বিপরীত পার্শ্বে কেন্দ্র O অবস্থিত । ∠BOC= 100° হলে ∠ ABC ও ∠ ABO এর মান হিসাব করে লিখি ।
সমাধানঃ

∆ABC সমদ্বিবাহু ত্রিভুজের AB=AC.বৃত্তের কেন্দ্র O , BC বাহুর বিপরীত পার্শ্বে অবস্থিত ।∠ABC ও ∠ ABO এর মাণ নির্ণয় করতে হবে ।
BOC = 100° ( প্রদত্ত)
এখন BAC বৃত্ত চাপের ওপর প্রবিদ্ধ কোণ∠BOC হল কেন্দ্রস্থ কোণ এবং কোণ ∠BAC হল পরিধিস্থ কোণ
∴∠ BOC=2∠BAC
সুতরাং , ∠BAC = `\frac{1}{2}` প্রবিদ্ধ কোণ ∠BOC
= `\frac{1}{2}` (360°-100°)
=`\frac{1}{2}` ✕ 260°
=130°
এখন , ত্রিভুজ ∆BAC এর ক্ষেত্রে ,
AB=AC
∴ ∠ABC = ∠ACB
আবার কোণ ∠BAC = 130°
সুতরাং , ∠ABC = ∠ACB = `\frac{(180°-∠BAC)}{2} = \frac{(180°-130°)}{2}` = 25°
ত্রিভুজ ∆OBC এর ক্ষেত্রে OB=OC
সুতরাং , ∠OBC = ∠OCB
আবার , কোণ ∠BOC = 100°
∴ ∠OBC =∠ OCB = `\frac{(180°-100°)}{2}`= 40°
সুতরাং ∠ABO = ∠ABC+∠OBC = 25°+40° =65°
∴ ∠ABC = 25° এবং ∠ABO = 65° (উত্তর)
2. পাশের চিত্রে ত্রিভুজ ABC এর পরিবৃত্তের কেন্দ্র O এবং ∠ AOC = 110° ; ∠ABC এর মাণ হিসাব করে লিখি ।
সমাধানঃ
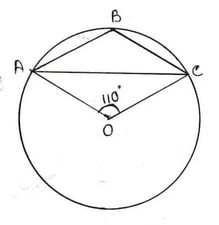
ABC বৃত্ত চাপের ওপর প্রবিদ্ধ কোণ ∠AOC কেন্দ্রস্থ কোণ এবং ∠ABC পরিধিস্থ কোণ
সুতরাং , ∠ABC = `\frac{1}{2}` প্রবিদ্ধ কোণ ∠AOC
∴ ∠ABC = `\frac{1}{2}`(360°-110°)= `\frac{1}{2}`✕250° = 125°
3.O কেন্দ্রীয় বৃত্তের ABCD হল একটি বৃত্তস্থ চতুর্ভুজ । DC বাহুকে P পর্যন্ত বর্ধিত করা হল । ∠BCP = 108 হলে ∠BOD এর মাণ হিসাব করে লিখি ।
সমাধানঃ

O কেন্দ্রীয় বৃত্তের ABCD হল একটি বৃত্তস্থ চতুর্ভুজ । DC বাহুকে P পর্যন্ত বর্ধিত করা হল
∠BCP = 108°
∴∠ BCD = 180°-108°=72°
এখন , BCD বৃত্ত চাপের ওপর কোণ ∠BOD কেন্দ্রস্থ কোণ এবং কোণ ∠BCD পরিধিস্থ কোণ
∴ ∠BOD = 2∠BCD = 2✕72°=144°
4. পাশের চিত্রে O কেন্দ্রীয় বৃত্তের ∠AOD =40° এবং ∠ACB = 35° ; ∠ BCO এবং ∠ BOD এর মাণ হিসাব করে লিখি ও উত্তরের সপক্ষে যুক্তি দিই ।
সমাধানঃ
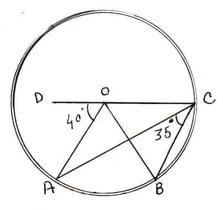
∠AOD = 40° এবং ∠ACB = 35°
বৃত্তটির কেন্দ্রস্থ কোণ ∠DOA এবং পরিধিস্থ কোণ ∠DCA
∴ ∠DOA = 2 ∠DCA
Or, ∠DCA = `\frac{1}{2}`∠DOA = `\frac{1}{2}`✕40° = 20°
∴ ∠BCO = ∠DCA+∠ACB= 20°+35° = 55°
আবার ,AB বৃত্ত চাপের ওপর AOB কেন্দ্রস্থ কোণ এবং ACB পরিধিস্থ কোণ
সুতরাং , ∠AOB = 2∠ACB = 2✕ 35° = 70°
∴ ∠BOD = ∠AOB+∠AOD = 70°+40°=110°
∴∠ BCO = 55° এবং ∠BOD = 110° ( উত্তর)
5. পাশের চিত্রে O কেন্দ্রীয় বৃত্তের ∠ APB = 80° হলে ∠AOB ও ∠COD এর মানের সমষ্টি নির্ণয় করি ও উভয় উত্তরের সপক্ষে যুক্তি দিই ।
সমাধানঃ

O কেন্দ্রীয় বৃত্তের ∠APB = 80°
∠AOB ও ∠COD এর মানের সমষ্টি নির্ণয় করতে হবে
A,D যুক্ত করা হল ।
AB বৃত্ত চাপের ওপর ∠AOB কেন্দ্রস্থ কোণ এবং ∠ADB পরিধিস্থ কোণ
∴ ∠AOB =2 ∠ADB—–(i)
আবার , CD বৃত্ত চাপের ওপর ∠COD কেন্দ্রস্থ কোণ এবং ∠CAD পরিধিস্থ কোণ
∴ ∠COD = 2∠CAD—–(ii)
এখন ∆APD ত্রিভুজে বহিঃস্থ কোণ ∠APB = ∠PAD+∠ADP [∵কোনো ত্রিভুজের একটি বহিঃস্থ কোণ,অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]
∴ ∠APB=∠PAD+∠ADP
বা, ∠APB=∠CAD+∠ADB [∵∠PAD =∠CAD এবং ∠ADP = ∠ADB ]
বা, ∠CAD+∠ADB = 80° [∵∠APB = 80°] —-(iii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই ,
∠AOB+∠COD
=2∠ADB+2∠CAD
=2(∠ADB+∠CAD)
=2✕ 80° [ (iii) নং সমীকরণ থেকে পাই ]
= 160°
6.পাশের ছবির মত C ও D কেন্দ্র বিশিষ্ট দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা PQ অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে । প্রমান করি যে ,
(i) ∠ PBQ = ∠CAD
(ii) ∠BPC = ∠BQD

C ও D কেন্দ্র বিশিষ্ট দুটি বৃত্ত, যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা PQ অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে । প্রমান করতে হবে যে ,
(i) ∠ PBQ = ∠ CAD
(ii) ∠ BPC = ∠ BQD
(i)

প্রমানঃ AP বৃত্ত চাপের ওপর ∠ACP কেন্দ্রস্থ কোণ এবং ∠ABP পরিধিস্থ কোণ
সুতরাং , ∠ABP = `\frac{1}{2}`∠ACP —– (1)
আবার , AQ বৃত্ত চাপের ওপর ∠ ADQ কেন্দ্রস্থ কোণ এবং ∠ ABQ পরিধিস্থ কোণ
∴ ∠ABQ = `\frac{1}{2}`∠ADQ —–(2)
এখন , ত্রিভুজ ∆ACP এর ক্ষেত্রে CA=CP [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠CAP= ∠CPA
∴ ∠ACP = (180º-2∠CAP) —-(3)
ত্রিভুজ ∆ADQ এর ক্ষেত্রে AD=DQ [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠DAQ = ∠DQA
∴ ∠ADQ = ( 180º -2∠DAQ) —–(4)
এখন , (1) নং ও (2) নং সমীকরণ যোগ করে পাই ,
∠ABP+∠ABQ
= `\frac{1}{2}`∠ACP+`\frac{1}{2}`∠ADQ
= `\frac{1}{2}`(∠ACP+∠ADQ)
= `\frac{1}{2}`{( 180°-2∠CAP)+(180°-2∠DAQ)} [(3) ও (4) নং সমীকরণ থেকে পাই ]
= `\frac{1}{2}`{360º -2(∠CAP+∠DAQ)}
=`\frac{1}{2}` {360º -2(180-∠CAD)}[∵∠PAQ=1 সরলকোণ ]
=`\frac{1}{2}` (360º -360º +2∠CAD)
= ∠CAD
∴ ∠ABP+ABQ =∠CAD
বা, ∠PBQ = ∠CAD [ প্রমাণিত ]
(ii)

অঙ্কনঃ C,B ; B,D যুক্ত করা হল ।
প্রমানঃ ACBD চতুর্ভুজের ক্ষেত্রে , BC =AC [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠CBA = ∠CAB —-(1)
আবার , BD = DA [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠DBA = ∠DAB —-(2)
(i) ও (ii) নং সমীকরণ যোগ করে পাই ,
∠CBA+∠DBA = ∠CAB+∠DAB
বা, ∠CBD=∠CAD —-(3)
আবার , ∠PBQ = ∠CAD [ পূর্বে প্রমাণিত ]
∴ ∠CBD = ∠PBQ
বা, ∠CBQ+∠DBQ = ∠CBP+∠CBQ
বা, ∠DBQ = ∠CBP—-( 4)
আবার , ∠DBQ = ∠DQB [∵ DB =DQ , একই বৃত্তের ব্যাসার্ধ ]—(5)
এবং , ∠CBP = ∠CPB [∵CB = CP , একই বৃত্তের ব্যাসার্ধ ]—(6)
∴ ∠DQB = ∠CPB [ 4,5 এবং 6 থেকে পাই ]
বা, ∠BPC = ∠BQD [ প্রমাণিত ]
7. ABC ত্রিভুজের পরিকেন্দ্র O ; প্রমান করি যে , ∠OBC+∠BAC = 90°
প্রমানঃ

∆ABC ত্রিভুজের পরিকেন্দ্র O ।
এখন , BC বৃত্ত চাপের ওপর ∠BOC কেন্দ্রস্থ কোণ এবং ∠BAC পরিধিস্থ কোণ
∴ ∠BAC = `\frac{1}{2}`∠BOC —-(1)
আবার , ত্রিভুজ ∆BOC এর ক্ষেত্রে ,
OB = OC [একই বৃত্তের ব্যসার্ধ ]
∴ ∠OBC =∠OCB
∴ ∠OBC = `\frac{( 180° –∠BOC)}{2}`- —(2)
এখন , ∠OBC+∠BAC
= `\frac{(180°-∠BOC)}{2} +\frac{1}{2}`∠BOC
= 90°- `\frac{1}{2}`∠BOC + `\frac{1}{2}`∠BOC
=90°
∴ ∠OBC+∠BAC =90°[ প্রমাণিত ]
8. দুটি সমান বৃত্ত একটি অপরটির কেন্দ্রগামী এবং বৃত্তদুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করলে , প্রমান করি যে ত্রিভুজ ∆BCD সমবাহু ত্রিভুজ ।

মনে করি, বৃত্ত দুটির কেন্দ্র যথাক্রমে P এবং Q
অঙ্কনঃ PA ,PB ,BQ,QA এবং PQ অঙ্কন করা হল ।
প্রমানঃ ∆APQ এর AP=PQ=AQ [ যেহেতু বৃত্ত দুটি সমান সুতরাং তাদের ব্যাসার্ধ সমান ]
∴ ∆APQসমবাহু ত্রিভুজ
∴ ∠APQ=∠AQP=60∘
অনুরূপে , ∆BPQ সমবাহু ত্রিভুজ ।
∴ ∠BPQ = ∠BQP = 60∘
এখন , ∠APB=∠APQ+∠BPQ
∴ ∠APB = 60°+60°
∴ ∠APB = 120°
অনুরূপে , ∠AQB = 120°
এখানে, AQB বৃত্তচাপের ওপর ∠APB কেন্দ্রস্থ কোণ এবং ∠ACB পরিধিস্থ কোণ
সুতরাং , ∠ACB = `\frac{1}{2}`✕ ∠APB = `\frac{1}{2}`✕ 120° = 60°
এবং , APB বৃত্তচাপের ওপর ∠AQB কেন্দ্রস্থ কোণ এবং ∠ADB পরিধিস্থ কোণ
∴ ∠ADB = `\frac{1}{2}`∠AQB = `\frac{1}{2}`✕120° = 60°
∴ ∆BCD ত্রিভুজে ∠BDC = ∠BCD = ∠CBD = 60°
∴ ∆BCD সমবাহু ত্রিভুজ (প্রমাণিত)
9. ABC ত্রিভুজের পরিবৃত্তের কেন্দ্র S এবং AD⊥BC হলে , প্রমান করি যে ∠BAD = ∠SAC
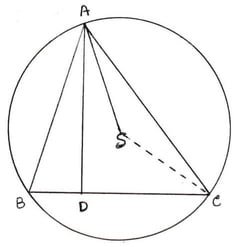
∆ABC ত্রিভুজের পরিবৃত্তের কেন্দ্র S এবং AD ⊥ BC । প্রমান করতে হবে ∠BAD = ∠SAC
অঙ্কনঃ S,C যুক্ত করা হল ।
প্রমানঃ ত্রিভুজ ∆ASC এর ক্ষেত্রে ,
AS =SC
∴ ∠SAC = ∠SCA
∴ ∠SAC= \frac{(180∘– ∠ASC)}{2} = 90 – `\frac{1}{2}`☓ ∠ ASC —-(i)
আবার , ∠ABC = `\frac{1}{2}`✕∠ASC [ যেহেতু একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন ]—-(ii)
∴ ∠SAC = 90-∠ABC [(i) ও (ii) থেকে পাই ]
আবার , ∠ABD+∠BAD = 90∘ [যেহেতু ∠ADB = 90∘ কারণ AD⊥BC ]
∴∠BAD = 90∘ – ∠ABD
⇒∠BAD = 90∘ – ∠ABC
∴ ∠SAC = ∠BAD
∴ ∠BAD = ∠SAC [ প্রমাণিত ]
10. O কেন্দ্রীয় বৃত্তের দুটি জ্যা AB ও CD পরস্পরকে P বিন্দুতে ছেদ করেছে । প্রমান করি যে ∠AOD +∠BOC = 2∠BPC
যদি ∠AOD ও ∠BOC পরস্পর সম্পূরক হয় তাহলে প্রমান করি যে , জ্যা দুটি পরস্পর লম্ব ।
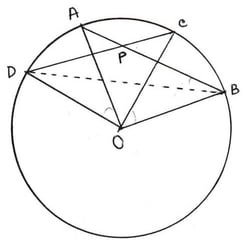
O কেন্দ্রীয় বৃত্তের দুটি জ্যা AB ও CD পরস্পরকে P বিন্দুতে ছেদ করেছে
প্রমান করতে হবে যে, ∠AOD +∠BOC = 2∠BPC
অঙ্কনঃ B,D যুক্ত করা হল ।
প্রমানঃ AD বৃত্তচাপের ওপর ∠AOD কেন্দ্রস্থ কোণ এবং ∠ABD পরিধিস্থ কোণ
∴ ∠AOD = 2∠ABD ———-(i)
আবার , BC বৃত্তচাপের ওপর ∠BOC কেন্দ্রস্থ কোণ এবং ∠BDC পরিধিস্থ কোণ
∴ ∠BOC = 2∠BDC ——(ii)
আবার ত্রিভুজ ∆PDB এর ক্ষেত্রে ,
∠PBD+∠PDB
= ∠ABD+ ∠BDC
= ∠BPC [ যেহেতু ত্রিভুজের বহিঃস্থ কোণ , অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]—(iii)
এখন (i) ও (ii) যোগ করে পাই ,
∠AOD+∠BOC = 2(∠ABD+∠BDC) = 2∠BPC [ (iii) থেকে পাই ]
∴ ∠AOD+∠BOC = 2∠BPC [ প্রমাণিত ]
আবার , ∠AOD এবং ∠BOC পরস্পর সম্পূরক হলে ,
∠AOD+∠BOC=180°
বা, 2∠BPC = 180° [∵ ∠AOD+∠BOC = 2∠BPC, পূর্বে প্রমাণিত ]
বা, ∠BPC = 90°
সুতরাং AB ও CD জ্যা দুটি পরস্পর লম্ব ।
11. O কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জ্যা কে বর্ধিত করলে তারা পরস্পরকে P বিন্দুতে ছেদ করলে , প্রমান করি যে , ∠AOC –∠BOD = 2∠BPC

O কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জ্যা কে বর্ধিত করলে তারা পরস্পরকে P বিন্দুতে ছেদ করে । প্রমাণ করতে হবে যে, ∠AOC –∠BOD = 2∠BPC
অঙ্কনঃ A,D যুক্ত করা হল ।
প্রমানঃ AC বৃত্তচাপের ওপর ∠AOC কেন্দ্রস্থ কোণ এবং ∠ADC পরিধিস্থ কোণ
∴ ∠AOC = 2∠ADC —-(i)
আবার , BD বৃত্তচাপের ওপর ∠BOD কেন্দ্রস্থ কোণ এবং ∠BAD পরিধিস্থ কোণ
∴ ∠BOD = 2 ∠BAD —-(ii)
আবার ত্রিভুজ ∆APD এর ক্ষেত্রে ,
∠ADC = ∠APD +∠PAD [∵ত্রিভুজের বহিঃস্থ কোণ , অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]
∴ ∠ADC-∠PAD = ∠APD —–(iii)
(i) থেকে (ii) বিয়োগ করে পাই ,
∠AOC – ∠BOD
= 2(∠ADC-∠BAD)
=2 (∠ADC-∠PAD) [∵∠BAD = ∠PAD]
= 2∠APD
= 2∠BPC [∵ ∠APD = ∠BPC]
∴ ∠AOC-∠BOD =2∠BPC [প্রমাণিত]
12.ABCD চতুর্ভুজের A বিন্দুকে কেন্দ্র করে একটি বৃত্ত অঙ্কন করা হল যেটি B , C ও D বিন্দু দিয়ে যায় । প্রমান করি যে CBD+CDB = `\frac{1}{2}`BAD ।

ABCD চতুর্ভুজের A বিন্দুকে কেন্দ্র করে একটি বৃত্ত অঙ্কন করা হল যেটি B , C ও D বিন্দু দিয়ে যায় । প্রমাণ করতে হবে ∠CBD+∠CDB =`\frac{1}{2}`∠BAD
অঙ্কনঃ বৃত্তের পরিধির ওপর E একটি বিন্দু , BE এবং DE অঙ্কন করা হল ।
প্রমানঃ ত্রিভুজ ∆BCD এর ক্ষেত্রে ,
∠CBD+∠CDB
= 180° –∠BCD [ যেহেতু ত্রিভুজের তিনটি কোণের সমষ্টি 180°]
= ∠BED [ যেহেতু বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি সম্পূরক ∴ ∠BCD+∠BED=180° ]
= `\frac{1}{2}`∠BAD [ BED বৃত্তচাপের ওপর ∠BAD কেন্দ্রস্থ কোণ এবং ∠BED পরিধিস্থ কোণ । এবং একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন ]
∴ ∠CBD+∠CDB = `\frac{1}{2}`∠BAD [প্রমাণিত]
13.ABC এর পরিকেন্দ্র O এবং OD ,BC বাহুর উপর লম্ব । প্রমাণ করি যে ∠BOD = ∠BAC ।
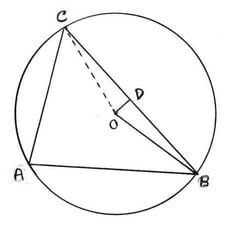
ABC এর পরিকেন্দ্র O এবং OD ,BC বাহুর উপর লম্ব ।
প্রমাণ করতে হবে , ∠BOD = ∠BAC
অঙ্কনঃ OC অঙ্কন করা হল ।
প্রমাণ: ∆BOD ও ∆COD এর ক্ষেত্রে,
∠ODB = ∠ODC =90∘ [ যেহেতু OD⊥ BC ]
OB = OC [ একই বৃত্তের ব্যাসার্ধ ]
OD সাধারণ বাহু
∴ ∆BOD ≅ ∆COD
∴ ∠BOD = ∠COD
∴ ∠BOD =`\frac{1}{2}`✕∠BOC = `\frac{1}{2}`✕2✕∠BAC = ∠BAC
∴∠BOD = ∠BAC [ প্রমাণিত ]
14. অতি সংক্ষিপ্ত প্রশ্ন (M.C.Q):
(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q):
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং PQ ব্যাস হলে , x এর মাণ কত ?
(a) 140°
(b) 40°
(c) 80°
(d) 20°

Ans: (d) 20°
সমাধানঃ ∠POR = 140°
∴ ∠ROQ = 180°-140° =40°
এখন , RQ বৃত্তচাপের উপর ∠ROQ কেন্দ্রস্থ কোণ এবং ∠RSQ পরিধিস্থ কোণ
∴ ∠RSQ=`\frac{1}{2}` ✕∠ROQ=`\frac{1}{2}`✕40°=20°
সুতরাং , x = 20°
(ii) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে , x এর মাণ
(a) 70°
(b) 60°
(c ) 40°
(d) 20°
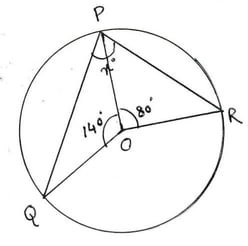
Ans: (a) 70°
সমাধানঃ
∠POQ =140° এবং ∠POR = 80°
∴ ∠QOR = 360°-(140°+80°) = 360°-220° = 140°
এখন , QR বৃত্তচাপের উপর ∠QOR কেন্দ্রস্থ কোণ এবং ∠QPR পরিধিস্থ কোণ
∠QPR = `\frac{1}{2}`✕∠QOR = `\frac{1}{2}`✕140° = 70°
∴ x = 70°
(iii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং BC ব্যাস হলে ,x এর মাণ
(a) 60°
(b) 50°
(c) 100°
(d) 80°

Ans: (b) 50°
সমাধানঃ OA =OB [একই বৃত্তের ব্যাসার্ধ ]
∴ ∠OAB = ∠OBA =50°
∴ ∠AOC = ∠OAB+∠OBA =50°+50° =100° [∵ কোনো ত্রিভুজের বহিঃস্থ কোণের মাণ অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]
আবার AC বৃত্তচাপের উপর ∠AOC কেন্দ্রস্থ কোণ এবং ∠ADC পরিধিস্থ কোণ
∴ ∠AOC = 2∠ADC
বা, ∠ADC = `\frac{1}{2}` ✕∠AOC
বা, ∠ADC = `\frac{1}{2}`✕100°
বা, ∠ADC = 50°
(iv) BC ত্রিভুজের O পরিকেন্দ্র । ∠OAB =50° হলে ∠ACB এর মাণ
(a) 50°
(b)100°
(c)40°
(d)80°

Ans: (c ) 40°
সমাধানঃ ∠OAB = 50°
∠OBA=50° [ OA=OB , একই বৃত্তের ব্যাসার্ধ ]
∴ ∠AOB = 180°-(∠OAB+∠OBA) =180°-(50°+50°) =80°
আবার , AB বৃত্তচাপের ওপর ∠AOB কেন্দ্রস্থ কোণ এবং ∠ACB পরিধিস্থ কোণ
∠ACB=`\frac{1}{2}`✕∠AOB [∵একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন ]
বা,∠ACB=`\frac{1}{2}`✕ 80°
বা, ∠ACB=40°
(v) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে , PQR এর মাণ
(a) 20°
(b) 40°
(c ) 60°
(d) 80°

Ans: (c ) 60°
ত্রিভুজ ∆OPQ তে , OP =OQ
∴ ∠OPQ =∠OQP =10°
∴ ∠POQ = 180°-(10°+10°) = 160°
আবার ,∆ORQ ত্রিভুজে OQ =OR [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠ORQ =∠OQR =40°
∴ ∠ROQ = 180°-(40°+40°) = 100°
এখন , ∠POR = ∠POQ – ∠ROQ = 160°-100° = 60°
(B) সত্য বা মিথ্যা লিখিঃ
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে , ∠AOB = 2∠ACD

উত্তরঃ মিথ্যা
কারণ AB এবং AD দুটি ভিন্ন বৃত্তচাপ ।
(ii) ABC ত্রিভুজের ক্ষেত্রের ভিতর O বিন্দু এমনভাবে অবস্থিত যে OA=OB এবং ∠AOB = 2∠ACB । O বিন্দুকে কেন্দ্র করে OA দৈর্ঘ্য এর ব্যাসার্ধ নিয়ে বৃত্ত অঙ্কন করলে C বিন্দু বৃত্তের ওপর অবস্থিত হবে ।
উত্তরঃ সত্য ।
কারণ ∠AOB = 2 ∠ACB সুতরাং একই বৃত্তচাপ AB এর ওপর অবস্থিত ∠AOB কেন্দ্রস্থ কোণ এবং ∠ACB পরিধিস্থ কোণ । সুতরাং C বিন্দু বৃত্তের ওপর অবস্থিত হবে ।
(C ) শূন্যস্থান পূরণ করিঃ
(i) একই চাপের উপর অবস্থিত বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের ___________ ।
উত্তরঃ অর্ধেক
(ii) O কেন্দ্রীয় বৃত্তে AB ও AC জ্যা দুটির দৈর্ঘ্য সমান । ∠APB ও ∠DQC বৃত্তস্থ কোণ হলে কোণ দুটির মান __________ ।
উত্তরঃ সমান
(iii) একটি সমবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O হলে , যে কোনো একটি বাহু দ্বারা উৎপন্ন সম্মুখ কেন্দ্রস্থ কোণের মান _______________ ।
উত্তরঃ 120°
15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A)
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র । ∠OAB = 40° , ∠ABC=120° , ∠BCO = y এবং ∠COA = x হলে x ও y এর মাণ নির্ণয় করো ।
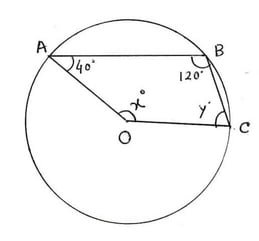
সমাধানঃ AC বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ ,প্রবিদ্ধ ∠AOC এবং পরিধিস্থ কোণ ∠ABC ।
∴ ∠ABC = `\frac{1}{2}`প্রবিদ্ধ ∠AOC [∵একই বৃত্তচাপের ওপর অবস্থিত পরিধিস্থ কোণ কেন্দ্রস্থ কোণের অর্ধেক ]
∴ 120° = `\frac{1}{2}`(360°-x)
⇒ 240°=360°-x
⇒ x=360°-240°
⇒ x=120°
∴ y=360°-(40°+120°+120°) = 360°-280°=80° [∵ চতুর্ভুজের চারটি কোণের সমষ্টি 360°]
∴x=120°, y=80° [উত্তর]
(ii) ABC ত্রিভুজের পরিকেন্দ্র O এবং D , BC এর মধ্যবিন্দু । ∠BAC = 40° হলে , ∠BOD এর মাণ নির্ণয় করো ।
সমাধানঃ

অঙ্কনঃ OC অঙ্কন করা হল ।
প্রমানঃ BAC বৃত্তচাপের ওপর ∠BAC পরিধিস্থ কোণ এবং ∠BOC কেন্দ্রস্থ কোণ ।
∠BOC =2∠BAC=2 ✕40° =80°
∆BOD ও ∆ COD এর ক্ষেত্রে ,
BD=DC [∵ D,BC এর মধ্যবিন্দু ]
OB = OC [ একই বৃত্তের ব্যাসার্ধ ]
OD সাধারণ বাহু
∴ BOD ≅ COD [বাহু-বাহু-বাহু শর্তানুসারে ]
∴ ∠BOD = ∠COD
আবার ∠BOC = 80°
∴ ∠BOD = ∠COD =40°
∴ ∠BOD=40° [উত্তর]
(iii) O কেন্দ্রীয় বৃত্তের উপর A ,B ,C তিনটি বিন্দু এমন ভাবে অবস্থিত যে AOCB একটি সামান্তরিক । ∠AOC এর মাণ নির্ণয় করি ।
সমাধানঃ
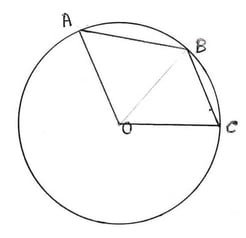
AOCB একটি সমান্তরিক ।
∴∠AOC = ∠ABC [∵ সামান্তরিকের বিপরীত কোণগুলি পরস্পর সমান ]—(i)
আবার , ∠ABC = `\frac{1}{2}`প্রবিদ্ধ ∠AOC [∵একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন ]—(ii)
(i) ও (ii) থেকে পাই ,
∴∠AOC=`\frac{1}{2}`প্রবিদ্ধ ∠AOC—(iii)
আবার, ∠AOC+প্রবিদ্ধ ∠AOC=360°
বা, `\frac{1}{2}`প্রবিদ্ধ ∠AOC+প্রবিদ্ধ ∠AOC=360° [(iii) থেকে পাই ]
বা, `\frac{3}{2}` ✕ (প্রবৃদ্ধ ∠AOC) = 360°
বা, 360°–∠AOC = 360° ✕ `\frac{2}{3}`
বা, ∠AOC =360°– 240°
বা, ∠AOC =120°
(iv) ABC সমদ্বিবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O এবং ∠ABC = 120° ; বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. হলে , AB বাহুর দৈর্ঘ্য নির্ণয় করি ।
সমাধানঃ
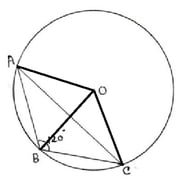
O,A;O,B;O,C যুক্ত করা হল ।
∆OAB এবং ∆OCB এর মধ্যে,
OA=OC [একই বৃত্তের ব্যাসার্ধ ]
OB সাধারণ বাহু
AB=BC [ ∆ABC সমদ্বিবাহু ত্রিভুজ ]
∴∆OAB ≅ ∆OCB [বাহু-বাহু-বাহু শর্তানুসারে]
∴ ∠OBA=∠OBC=60° [∵∠ABC =120° ]
আবার, ∠OAB=∠OBA=60° [∵OA=OB একই বৃত্তের ব্যাসার্ধ]
∴ ∠AOB=60° [∵ ত্রিভুজের তিনটি কোণের সমষ্টি 180° ]
∴ ত্রিভুজ AOB -এর ∠OAB=∠OBA=∠AOB=60°
∴ AOB সমবাহু ত্রিভুজ ।
∴ OA=OB=AB =5 সেমি.
∴ AB=5 সেমি.[উত্তর]
(V) A ও B কেন্দ্রীয় বৃত্তদ্বয় C ও D বিন্দুতে ছেদ করে । A কেন্দ্রীয় বৃত্তের উপর অপর বৃত্তের কেন্দ্র B অবস্থিত । ∠CQD =70° হলে ∠CPD এর মান নির্ণয় করি ।
সমাধানঃ
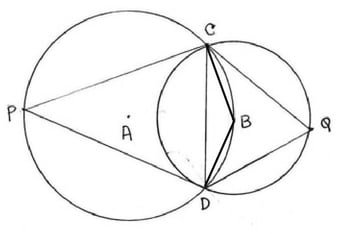
B,C ; B,D যুক্ত করা হল ।
CD বৃত্তচাপের ওপর ∠CBD কেন্দ্রস্থ কোণ এবং ∠CQD পরিধিস্থ কোণ
∴ ∠CBD =2✕∠CQD =2✕70°=140°
আবার, ∠CBD+∠CPD=180° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
⇒ ∠CPD= 180°–∠CBD
⇒ ∠CPD=180°-140°
⇒ ∠CPD=40° [উত্তর]
Note: এই আর্টিকেলের ব্যাপারে তোমার মতামত জানাতে নীচে দেওয়া কমেন্ট বক্সে গিয়ে কমেন্ট করতে পারো। ধন্যবাদ।