প্রিয় ছাত্রছাত্রীরা, এই আর্টিকেলে আমরা অষ্টম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট ৮ (Class 8 Mathematics Model Activity Task Part 8 Combined) এর সমস্ত প্রশ্ন ও উত্তর নিয়ে এসেছি । ২০২১ এর জুলাই থেকে অক্টোবর মাস পর্যন্ত যে সমস্ত মডেল অ্যাক্টিভিটি টাস্ক দেওয়া হয়েছিল সেখান থেকে বাছাই করা করা কিছু প্রশ্ন নিয়ে এবার তোমাদের কম্বাইন্ড অ্যাক্টিভিটি টাস্ক করতে দেওয়া হয়েছে ।
Class 8 Mathematics Model Activity Task Part 8 Combined
২০২১ এর এটাই সর্বশেষ অ্যাক্টিভিটি টাস্ক । এই অ্যাক্টিভিটি টাস্কে ৫০ নম্বরের প্রশ্ন দেওয়া রয়েছে যেগুলো তোমাদের সমাধান করে বিদ্যালয়ে জমা দিতে বলা হয়েছে । এর উপর ভিত্তি করেই সম্ভাবত তোমরা পরবর্তী শ্রেণীতে উত্তীর্ণ হবে । সুতরাং, খুবই মন দিয়ে তোমরা নিচের প্রশ্নোত্তর গুলি পড়বে এবং লিখবে ।
মডেল অ্যাক্টিভিটি টাস্ক Part 8 (Combined), October 2021
গণিত (পূর্ণমান ৫০)
অষ্টম শ্রেণী
Class 8 Mathematics Model Activity Task Part 8 Solution :
প্রশ্নগুলির উত্তর লেখাে :
1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs) :
(i) দুটি পরস্পরছেদী সরলরেখার একজোড়া বিপ্রতীপ কোণ পরস্পর পূরক কোণ হলে, অপর জোড়া বিপ্রতীপ কোণ দুটির প্রত্যেকটির মান হবে
(a) 180°
(b) 45°
(c) 90°
(d) 135°
উত্তর: (d) 135°
(ii) দূরত্ব স্থির থাকলে যদি গতিবেগ দ্বিগুণ হয় তাহলে সময়
(a) অর্ধেক হবে
(b) দ্বিগুণ হবে
(c) অপরিবর্তিত থাকবে
(d) তিনগুণ হবে
উত্তর: (a) অর্ধেক হবে
(iii) 20 জন একটি কাজ 8 দিন করে। 10 জন ওই কাজটির অংশ করবে
(a) 32 দিনে
(b) 8 দিনে
(c) 10 দিনে
(d) 2 দিনে
উত্তর: (b) 8 দিনে
(iv) এক ধরনের পিতলে তামা ও দস্তার পরিমাণের অনুপাত 5:2; এই ধরনের 28 কিগ্রা. পিতলে তামা আছে
(a) 8 কিগ্রা,
(b) 11.2 কিগ্রা
(c) 16.8 কিগ্রা
(d) 20 কিগ্রা.
উত্তর: (d) 20 কিগ্রা.
(v) বুলু ও তথাগত একটি কাজ একা একা যথাক্রমে 20 দিনে ও 30 দিনে করতে পারে। দুজনে একসঙ্গে 1 দিনে করে
(a) (1/2 + 1/3) অংশ
(b) (20 + 30) অংশ
(c) (1/20 + 1/30) অংশ
(d) (1/20 – 1/30) অংশ
উত্তর: (c) (1/20 + 1/30) অংশ
(vi)
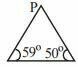
চিত্রে ,
(a) QR<PR
(b) PR<PQ
(c) QR<PQ
(d) QR > PQ
উত্তর: (d) QR > PQ
(vii) (2m + 5n) (2m – 5n) এবং mn (2m – 5n) সংখ্যামালা দুটির গ.সা.গু হলাে
(a) 1
(b) mn (2m+5n) (2m-5n)
(c) (2m+5n)
(d) (2m-5n)
উত্তর: (d) (2m-5n)
2. সত্য/মিথ্যা লেখাে (T/F) :
(i) 30 লিটার ডেটল-জলে জল ও ডেটলের পরিমাণের অনুপাত 5:1, ইহাতে ডেটল আছে 25 লিটার।
উত্তর: মিথ্যা
(ii) (27x³ – 343y³) সংখ্যামালাটি (3x – 7y) দ্বারা বিভাজ্য।
উত্তর: সত্য
(iii) 2a²b এবং 4ab²-এর গ.সা.গু হলাে 4a²b²।
উত্তর: মিথ্যা
(iv) `\frac{x^2}a+\frac{a^2}x=\frac{x^2+a^2}{a+x}`
উত্তর: মিথ্যা
(v) 
উত্তর: মিথ্যা
(vi) হারুণচাচা 1 দিনে কোনাে কাজের 1/10 অংশ করেন। সম্পূর্ণ কাজটি করতে হারুণচাচার 10 দিন সময় লাগবে।
উত্তর: সত্য
(vii) 2.25 টাকা, 5 টাকার শতকরা 4.5
উত্তর: মিথ্যা
3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন :
(i)
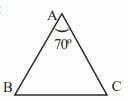
চিত্রে, ΔABC-এর AB=AC এবং ∠BAC = 70°। ∠ABC এবং ∠ACB-এর পরিমাপ নির্ণয় করাে।
উত্তর:

দেওয়া আছে, AB = AC এবং ∠BAC = 70°
∴ ∠ACB = ∠ABC
অতএব, ∠ABC+∠BCA+∠CAB = 180°
বা, ∠ABC+∠ABC+70° = 180°
বা, 2 ∠ABC = 110°
বা, ∠ABC = 110°/2 = 55°
∴ ∠ACB = 55°
(ii) দুটি সমান মাপের কৌটায় মিশ্র চায়ে আসাম চা ও দার্জিলিং চায়ের পরিমাণের অনুপাত যথাক্রমে 5:18 এবং 2:3। কোন কৌটায় আসাম চায়ের পরিমাণ বেশী আছে?
উত্তর: প্রথম কৌটায় আসাম চা : দার্জিলিং চা = 5:18
দ্বিতীয় কৌটায় আসাম চা : দার্জিলিং চা = 2:3
∴ প্রথম কৌটায় আসাম চায়ের আনুপাতিক ভাগহার = `\frac5{5+18}` = `\frac5{23}`
এবং দ্বিতীয় কৌটায় আসাম চায়ের আনুপাতিক ভাগহার = `\frac2{2+3}` = `\frac2{5}`
∴ তুলনা করে পাই,
প্রথম কৌটা = `\frac5{23}` = `\frac{5\times5}{23\times5}` = `\frac{25}{115}`
দ্বিতীয় কৌটা = `\frac2{5}` = `\frac{2\times23}{5\times23}` = `\frac{46}{115}`
অতএব, 46 > 25
∴ দ্বিতীয় কৌটায় আসাম চায়ের পরিমাণ বেশী।
(iii) গণিতের ভাষায় সমস্যাটি হলাে
| গরুর সংখ্যা (টি) | সময় (দিন) | খড়ের পরিমাণ (কাহন) |
| 8 | 15 | 4 |
| 10 | 72 | x |
(a) সময় স্থির থাকলে গােরুর সংখ্যার সঙ্গে খড়ের পরিমাণের সমানুপাত সম্পর্কটি লেখাে।
উত্তর: সময় স্থির থাকলে গােরুর সংখ্যা বাড়লে খড়ের পরিমাণ বাড়বে এবং গরুর সংখ্যা কম্লে খড়ের পরিমাণ কমবে।
∴ সময় স্থির থাকলে গরুর সংখ্যার সাথে খড়ের পরিমানের সরল সম্পর্ক।
(b) গােরুর সংখ্যা স্থির থাকলে সময়ের সঙ্গে খড়ের পরিমাণের সমানুপাত সম্পর্কটি লেখাে।
উত্তর: গরুর সংখ্যা একই থাকলে সময় বাড়লে খড়ের পরিমাণ বাড়বে এবং সময় কমলে খড়ের পরিমাণ বাড়বে।
∴ গরুর সংখ্যা স্থির থাকলে সময়ের সাথে খড়ের পরিমাণের সরল সম্পর্ক।
(iv) x²+px+q বীজগাণিতিক সংখ্যামালায় p = a + b এবং q = a × b হলে, সংখ্যামালাটির উৎপাদক দুটি লেখাে।
উত্তর: x2+px+q সংখ্যামালায় p = a+b এবং q = a×b বসিয়ে পাই,
x2+px+q
= x2 + (a+b)x + a×b
= x2 + ax + bx + a×b
= x(x+a)+b(x+a)
= (x+a)(x+b)
4. (i) `\frac{\x}2=\frac1{2x}+1` হলে, `\x^3-\frac1{x^3}` এর মান নির্ণয় করো।
উত্তর:
`\frac{\x}2=\frac1{2x}+1`
`\Rightarrow\frac x2-\frac1{2x}=1`
`\Rightarrow\frac1{2}\left(x-\frac1x\right)=1`
` \Rightarrow \left(x-\frac1x\right)=2`
`\therefore\x^3-\frac1{x^3}`
`=\left(x\right)^3-\left(\frac1{x}\right)^3`
`=\left(x-\frac1x\right)^3+3.\cancel x.\frac1{\cancel x}\left(x-\frac1x\right)`
`=2^3+3.2`
`=8+6`
`=14`
(ii) ভাগ করাে : (m² – 5m + 6 )-কে (m – 3) দিয়ে
উত্তর:
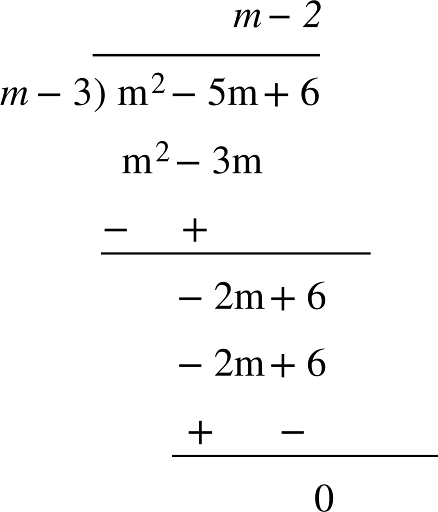
Read Also:
Class 8 English Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8
Class 8 Bengali (বাংলা) Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8
Class 8 পরিবেশ ও বিজ্ঞান Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8
Class 8 পরিবেশ ও ইতিহাস Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8
Class 8 পরিবেশ ও ভূগোল Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8
Class 8 স্বাস্থ্য ও শারীরশিক্ষা Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8
Class 1-10 Combined Activity Task / মডেল অ্যাক্টিভিটি টাস্ক Part 8
5. ক্লাসের ছাত্রছাত্রীরা কোন কোন খেলা কতজন করে পছন্দ করে শতকরায় তার তালিকা হলাে (একজন কেবলমাত্র একটি খেলাই পছন্দ করবে)
| খেলা | খেলা পছন্দ করা ছাত্রছাত্রীর সংখ্যা (শতকরায়) |
| ক্রিকেট | 60 |
| ফুটবল | 30 |
| ব্যাডমিন্টন | 10 |
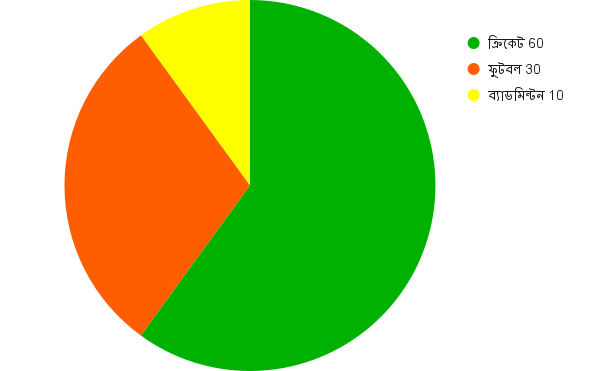
পাই চিত্রে, যে বৃত্তকলাগুলি তথ্যটির অংশগুলিকে বােঝাবে সেই বৃত্তকলাগুলির কেন্দ্রীয় কোণগুলি নির্ণয় করাে এবং তথ্যটির পাই চিত্র অঙ্কন করাে
উত্তর:
পাইচিত্রের মোট কেন্দ্রীয় মান = 360°
ক্রিকেট নির্দেশক বৃত্তকলার কেন্দ্রীয় মান
= `360^\circ\times\frac{60}{60+30+10}`
= `36\cancel0^\circ\times\frac{6\cancel0}{1\cancel0\cancel0}`
= 216°
∴ ফুটবল নির্দেশক বৃত্তকলার কেন্দ্রীয় মান `=36\cancel0^\circ\times\frac{3\cancel0}{1\cancel0\cancel0}=108`
এবং ব্যাডমিন্টন নির্দেশক বৃত্তকলার কেন্দ্রীয় মান `=36\cancel0^\circ\times\frac{1\cancel0}{1\cancel0\cancel0}=36^\circ`
6. (i) যুক্তি দিয়ে প্রমাণ করাে যে, ত্রিভুজের কোনাে একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয় সেটির পরিমাপ অন্তঃস্থ বিপরীত কোণ দুটির পরিমাপের যােগফলের সমান।
উত্তর:
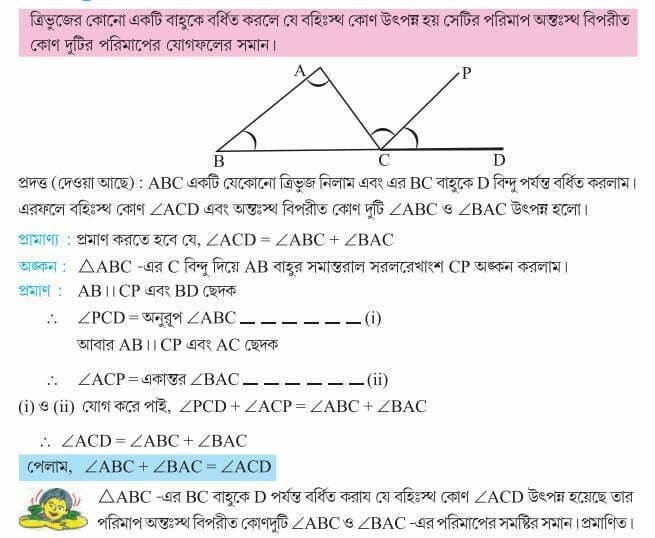
(ii) প্রমান করবে, যে কোনাে ত্রিভুজের তিনটি কোণের সমষ্টি 180° |
উত্তর:
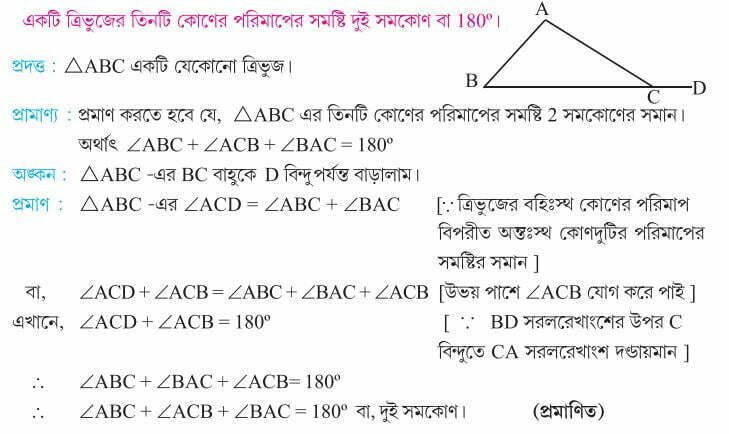
7.5 অশ্বক্ষমতাসম্পন্ন একটি পাম্প 36000 লিটার জল ৪ ঘণ্টায় উপরে তুলতে পারে। 7 অশ্বক্ষমতা সম্পন্ন পাম্পের 63000 লিটার জল তুলতে কত সময় লাগবে ত্রৈরাশিক পদ্ধতিতে নির্ণয় করাে।
উত্তর:
| পাম্প (অশ্বক্ষমতাসম্পন্ন) | জল (লিটার) | সময় (ঘণ্টায়) |
| 5 | 36000 | 8 |
| 7 | 63000 | x (ধরি) |
∴ পাম্পের সাথে সময়ের ব্যস্ত সম্পর্ক এবং জলের সাথে সময়ের সরল সম্পর্ক।
∴ নির্ণেয় সময় (x) = `\overset2{\cancel8}\times\frac5{\cancel7}\times\frac{\overset{\cancel7}{\cancel{63}}\cancel{000}}{\underset{\cancel4}{\cancel{36}}\cancel{000}}` = 10 ঘণ্টা
∴ জল তুলতে 10 ঘণ্টা সময় লাগবে।
Note: এই আর্টিকেলের ব্যাপারে তোমার মতামত জানাতে নীচে দেওয়া কমেন্ট বক্সে গিয়ে কমেন্ট করতে পারো। ধন্যবাদ।

Thanks
You are Welcome
Thank you
Thank you for your help 😄😄😄
Good
Thank you so much for all of you help
Thank you for your help
🤗🤗🤗🤗🤗🤗🤗🤗🤗
Thank you👌👌👌
Thank you for halp
Thank you for help
Thank you so much
Thanks 🙏🙏
Very nice app
Good 👍